If Saturn could fit in a bathtub, would it float? Use the planetary data in Appendix A to calculate the density (mass/volume) of Earth, Mars, Jupiter, and Saturn. What are the differences? Can you explain them? If an object has a density less than 1000 kg/m³, it will float in water. Would any of these planets float (assuming a big enough container of water!)? (Your calculated values of the density should assume spherical planets. The density values in Table A.3 do not make this assumption and are therefore more accurate.) 

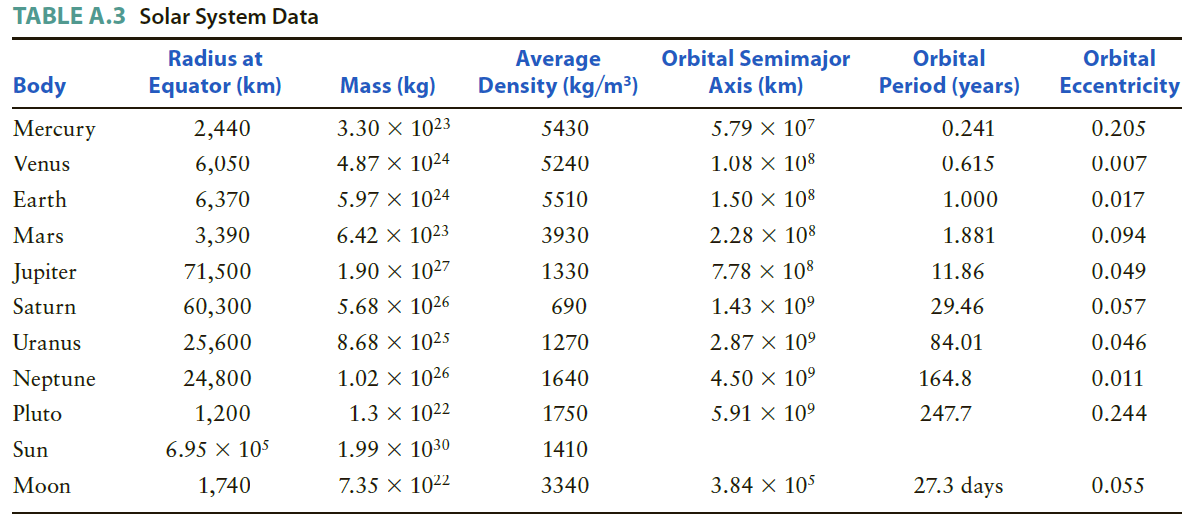
TABLE A.3 Solar System Data Orbital Semimajor Axis (km) Radius at Orbital Orbital Average Density (kg/m) Mass (kg) Period (years) Body Equator (km) Eccentricity 3.30 1023 5430 5.79 107 Mercury 2,440 0.241 0.205 4.87 1024 1.08 108 Venus 6,050 5240 0.615 0.007 1.50 108 Earth 5.97 X 1024 1.000 6,370 5510 0.017 3,390 6.42 1023 2.28 108 Mars 3930 1.881 0.094 7.78 108 71,500 1.90 1027 11.86 0.049 Jupiter 1330 29.46 1.43 10 Saturn 60,300 5.68 1026 690 0.057 2.87 10 8.68 1025 Uranus 25,600 1270 84.01 0.046 1.02 1026 1640 4.50 10 Neptune 24,800 164.8 0.011 Pluto 5.91 10 1,200 1.3 1022 1750 247.7 0.244 1.99 1030 Sun 6.95 105 1410 27.3 days 7.35 1022 3.84 105 1,740 3340 Moon 0.055