Question: Keplers second law, the statement that a planet sweeps out equal areas in equal times, can be derived by a geometrical argument. To see how

Kepler€™s second law, the statement that a planet sweeps out equal areas in equal times, can be derived by a geometrical argument. To see how one might construct such a geometrical proof, consider the simpler case of a planet moving with constant velocity as shown in Figure Q5.6. The points A, B, C, . . . are spaced at equal time intervals. Show that this planet obeys Kepler€™s second law; that is, show that it sweeps out equal areas in equal times.

Figure Q5.6

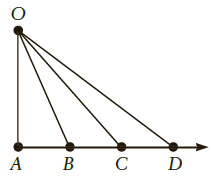
A B C D

Step by Step Solution

★★★★★

3.40 Rating (159 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The area of a triangle is one half the base times the h... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related College Physics Reasoning Questions!

FIGURE CP34.80 shows a light ray that travels from point A to point B. The ray crosses the boundary at position x, making angles 1 and 2 in the two media. Suppose that you did not know Snell??s...

Keplers second law states: The radius vector from the sun to a planet sweeps out equal areas in equal times. Show that this law follows directly from the law of conservation of angular momentum and...

Show that the relativistic form of Newtons Second Law becomes -3/2 2-3/2 du F= m dt

Australian Catholic University Mount Saint Mary Semester 2 2021 Geometry MATHZOS Assignment Part 3 Due: Friday 22"'1 October 2021 Assignment for: 12. An ellipse has its foci at (4.0) and (7.0), and...

14. Johannes Kepler (15711630AD) developed 3 revolutionary laws (pun intended) about planetary motion. Those laws are given below, although we don't need the second one. The orbits of planets are...

A circle is a special ellipse, one with both foci at the same point. The eccentricity of a circle is 0. The value of the eccentricity of an orbit may run from 0 to almost 1. Match the letter of the...

Hello, need help with this lab. Very math orientated Rowan Introduction to Astronomy Lab 4 I An Introduction to Kepler's 3 Laws Name: Score: AObjectives l> Reproducing ellipses via the...

Here is the references: &7Issues in Space Exploration: Hazards and Criticisms There are several concerns and criticisms regarding the exploration of space. A few of these will be discussed in this...

LEARNING ACTIVITY SHEET Kepler's Law of Planetary Motion Background Information for the Learners (BIL) In the early 1600s, Johannes Kepler proposed three laws of planetary motion. Kepler was able to...

Using "On the Spectrum of Hydrogen" by Niels Bohr -What is the main idea of the Author's argument? What is the main essence of the piece? -What ways does the author use to propose and support their...

N, N-Diethyl-m-toluamide (DEFT) is the active ingredient in many insect- repellent preparations. Flow might you synthesize this substance fromm-bromotoluene? . CH2CH3 N,N-Diethyl-m-toluamide CH-CH

In addition to managerial style, a manager's cognitive make up also affects their effectiveness. Justify your answer with suitable examples.

Which amongst the following version of Bootstrap uses the flat design? Bootstrap Bootstrap 3 Bootstrap 4 None of the above

Answer the questions below. a. Why do holders of mortgage-backed securities (MBS) suffer more when interest rates in the economy fall so as to trigger mortgage refinancing? b. Why do MBS lose more...

Solar cells convert the energy of incoming light to electric energy; a good quality cell operates at an efficiency of 15%. Each person in the United States uses energy (for lighting, heating,...

Figure Q16.6 shows a standing wave on a string that is oscillating at frequency f o . How many antinodes will there be if the frequency is doubled to 2f o ? Explain. FIGURE Q16.6

Denver, Colorado, has an oldies station that calls itself "KOOL 105." This means that they broadcast radio waves at a frequency of 105 MHz. Suppose that they decide to describe their station by its...

Recapitalization, Debt-to-Equity, and ROE An institutional investor believes that the company he has invested in should increase its leverage to improve the return on its stock. Currently, the...

pls answer all parts Aa 24. Company valuation Chiara Company's management has made the projections shown in Table 19.5. Use this table as a starting point to value the company as a whole. The WACC...

Starware Software was founded last year to develop software for gaming applications. The founder initially invested $700,000 and received 10 million shares of stock. Starware now needs to raise a...