Write an MIPS assembly language program to calculate the product of the signed integers A and B. State if you are using the approach given in 3.4.4 or 3.4.5.

Problem 3.4.4

When multiplying signed numbers, one way to get the correct answer is to convert the multiplier and multiplicand to positive numbers, save the original signs, and then adjust the final value accordingly. Using a table similar to that shown in Figure 3.7, calculate the product of A and B using the hardware described in Figure 3.4. You should show the contents of each register on each step, and include the step necessary to produce the correctly signed result. Assume A and B are stored in 6-bit sign-magnitude format.

Figure 3.7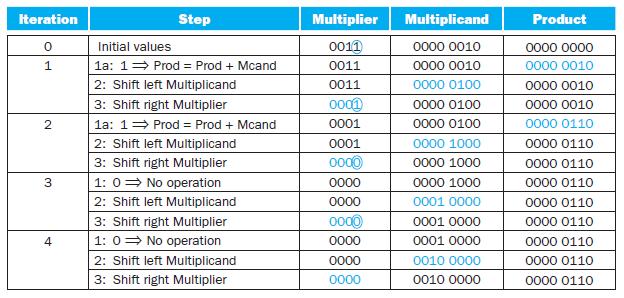

Figure 3.4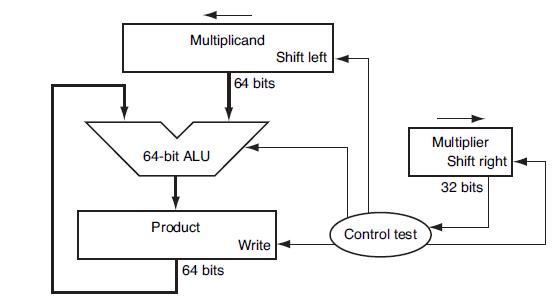

Problem 3.4.5

When shifting a register one bit to the right, there are several ways to decide what the new entering bit should be. It can always be a zero, or always a one, or the incoming bit could be the one that is being pushed out of the right side (turning a shift into a rotate), or the value that is already in the leftmost bit can simply be retained (called an arithmetic shift right, because it preserves the sign of the number that is being shift). Using a table similar to that shown in Figure 3.7, calculate the product of the 6-bit two’s complement numbers A and B using the hardware described in Figure 3.6. The right shifts should be done using an arithmetic shift right. Note that the algorithm described in the text will need to be modified slightly to make this work—in particular, things must be done differently if the multiplier is negative. You can find details by searching the web. Show the contents of each register on each step.

Figure 3.6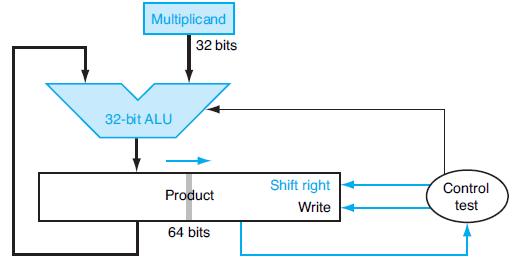

The following table shows pairs of octal numbers.

Iteration 0 1 2 3 4 Step Initial values 1a: 1 Prod Prod + Mcand 2: Shift left Multiplicand 3: Shift right Multiplier 1a: 1 Prod = Prod + Mcand 2: Shift left Multiplicand 3: Shift right Multiplier 1: 0 No operation 2: Shift left Multiplicand 3: Shift right Multiplier 1: 0 No operation 2: Shift left Multiplicand 3: Shift right Multiplier Multiplier 0011 0011 0011 0001 0001 0001 0000 0000 0000 0000 0000 0000 0000 Multiplicand 0000 0010 0000 0010 0000 0100 0000 0100 0000 0100 0000 1000 0000 1000 0000 1000 0001 0000 0001 0000 0001 0000 0010 0000 0010 0000 Product 0000 0000 0000 0010 0000 0010 0000 0010 0000 0110 0000 0110 0000 0110 0000 0110 0000 0110 0000 0110 0000 0110 0000 0110 0000 0110