Question: Consider a 5-bit floating-point representation based on the IEEE floating-point format, with one sign bit, two exponent bits (k = 2), and two fraction bits

Consider a 5-bit floating-point representation based on the IEEE floating-point format, with one sign bit, two exponent bits (k = 2), and two fraction bits (n = 2).
The exponent bias is 2²⁻¹ − 1= 1.
The table that follows enumerates the entire nonnegative range for this 5-bit floating-point representation. Fill in the blank table entries using the following directions:

e : The value represented by considering the exponent field to be an unsigned integer

E : The value of the exponent after biasing 2E: The numeric weight of the exponent

f : The value of the fraction

M : The value of the significand 2E ×M: The (unreduced) fractional value of the number

V : The reduced fractional value of the number

Decimal: The decimal representation of the number

Express the values of 2^E, f , M, 2^E × M, and V either as integers (when possible) or as fractions of the form ^x/_y , where y is a power of 2. You need not fill in entries marked -.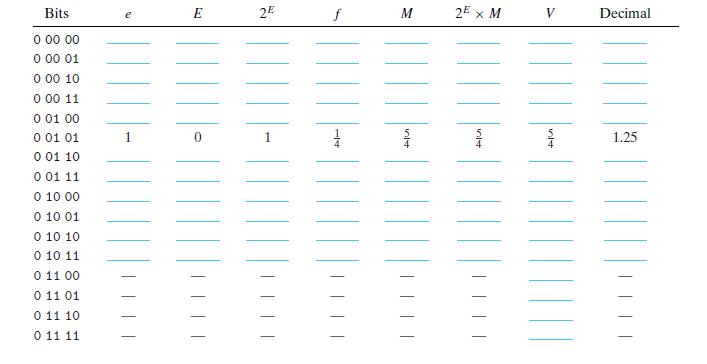 Bits 0 00 00 0 00 01 0 00 10 0 00 11 0 01 00 0 01 01 0 01 10 0 01 11 0 10 00 0 10 01 0 10 10 0 10 11 0 11 00

Bits 0 00 00 0 00 01 0 00 10 0 00 11 0 01 00 0 01 01 0 01 10 0 01 11 0 10 00 0 10 01 0 10 10 0 10 11 0 11 00 0 11 01 0 11 10 0 11 11 E 0 2E H f 1 M inl+ 2E x M FIS 2 FIS Decimal 1.25

Step by Step Solution

★★★★★

3.35 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Working through floatingpoint representations for very ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Computer Systems A Programmers Perspective Questions!

A relatively small privately owned coal-mining company has the sales results summarized below. Determine the annual percentage depletion for the coal mine. Assume the company's taxable income is...

Consider the following 9-bit floating point representation based on the IEEE floating point format: The most-significant bit is the sign bit. The next four bits are the exponent. The...

Assume that it takes four hours of labor time to paint a room and two hours to sand a floor. If two workers each spend 24 hours painting, a. How many rooms could be painted? 12 room(s) b. If a...

Consider a 7-bit floating-point representation based on the IEEE floating-point format, with one sign bit, three exponent bits (k 3), and three fraction bits (n 3). The exponent bias is 231-1 3. The...

Consider a 9-bit floating-point representation based on the IEEE floating-point format, with one sign bit, 3 exponent bits and 5 fraction bits. The exponent bias follows the IEEE standard. Convert...

Consider a 8-bit floating-point representation based on the IEEE floating-point format, with one sign bit, 3 exponent bits and 4 fraction bits. The exponent bias follows the IEEE standard. Convert...

solve these questions Consider a 7-bit floating-point representation based on the IEEE floating-point format, with one sign bit, three exponent bits (k 3), and three fraction bits (n = 3). The...

Assembly language class 2.86 Consider a 16-bit floating-point representation based on the IEEE floating-point format, with one sign bit, seven exponent bits (k7), and eight fraction bits (n 8). The...

Consider a 5-bit floating-point representation based on the IEEE floating-point format, with one sign bit, three exponent bits (k = 2), and three fraction bits (n = 2). The exponent bias is 2^2-1 - 1...

Consider a 8-bit floating-point representation based on the IEEE floating-point format, with one sign bit, 4 exponent bits and 3 fraction bits. The exponent bias follows the IEEE standarod. Interpret...

The concept of financial leverage was introduced in Chapter 7 and expanded on in Chapter 11. In Exercise 7.15 you were asked to describe the risks associated with financial leverage. You should now...

Read the following extract and answer the questions that follow: When a Scented Candle Just Won't Do A fragrance called green tea blows through the corridors of Sonesta hotels worldwide courtesy of...

Compare the cost model vs . revaluation model, including pros, cons, and theoretical implications ( e . g . , relevance vs . reliability ) .

A sawtooth wave has peak-to-peak amplitude of 24V and a fundamental frequency of 2 kHz. Use the results in Figure 134 to write an expression for the first four nonzero terms in the Fourier series and...

Show that if d(n) is O( f (n)) and e(n) is O(g(n)), then the product d(n)e(n) is O( f (n)g(n)).

Show that (n+1) 5 is O(n 5 ).

Show that 2 n+1 is O(2 n ).

On January 1 of this year, Ikuta Company issued a bond with a face value of $125,000 and a coupon rate of 8 percent. The bond matures in 3 years and pays interest every December 31. When the bond was...

which of the following describes an account that would be debited when applying manufacturing overhead? - raw materials inventory - work in process inventory - finished goods inventory -...

Direct Materials, Direct Labor, and Factory Overhead Cost Variance Analysis Santiago Inc. processes a base chemical into plastic. Standard costs and actual costs for direct materials, direct labor,...