(a) The transfer function for the right-side rectangular-rule integrator was found in Problem 2.2-1 to be Y(z)/X(z) = Tz/(z −1) . We would suspect that the reciprocal of this transfer function should yield an approximation to a differentiator. That is, if w(kT) is a numerical derivative of x(t) at t = kT,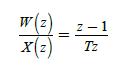

Write the difference equation describing this differentiator.

(b) Draw a figure similar to those in Fig. P2.2-1 illustrating the approximate differentiation.

(c) Repeat part (a) for the left-side rule, where W(z)/X(z) = T / (z −1).

(d) Repeat part (b) for the differentiator of part (c).

Problem 2

The trapezoidal rule (modified Euler method) for numerical integration approximates the integral of a function x(t) by summing trapezoid areas as shown in Fig. P2.2-2. Let y(t) be the integral of x(t) .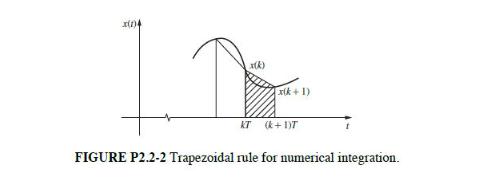

W(z) 2-1 Tz