Consider three ((T-1) times T) matrices defined in (8.15) as follows: (C_{1}=) the first ((T-1)) rows of
Question:
Consider three \((T-1) \times T\) matrices defined in (8.15) as follows: \(C_{1}=\) the first \((T-1)\) rows of \(\left(I_{T}-\bar{J}_{T}\right), C_{2}=\) the first-difference operator, \(C_{3}=\) the forward orthogonal deviations operator which subtracts the mean of future observations from the first \((T-1)\) observations. This last matrix is given by Arellano and Bover
(1995) as \[\begin{aligned}
& C_{3}=\operatorname{diag}\left[\frac{T-1}{T}, \ldots, \frac{1}{2}\right]^{1 / 2}
\end{aligned}\]
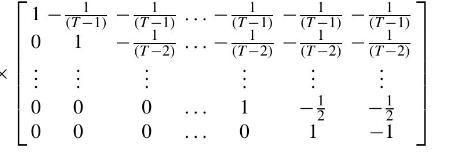
Verify that each one of these \(C\) matrices satisfies
(a) \(C_{j} \iota_{T}=0\) for \(j=1,2,3\).
(b) \(C_{j}^{\prime}\left(C_{j} C_{j}^{\prime}\right)^{-1} C_{j}=I_{T}-\bar{J}_{T}\), the Within transformation, for \(j=1,2,3\).
(c) For \(C_{3}\), show that \(C_{3} C_{3}^{\prime}=I_{T-1}\) and \(C_{3}^{\prime} C_{3}=I_{T}-\bar{J}_{T}\). Hence \(C_{3}=\left(C^{\prime} C\right)^{-1 / 2} C\) for any upper triangular \(C\) such that \(C \iota_{T}=0\).
\[H=\left[\begin{array}{c}
C \tag{8.15}\\
\iota_{T}^{\prime} / T
\end{array}\right]\]
Step by Step Answer:






