Prediction in the one-way random effects model.

(a) For the predictor \(y_{i, T+S}\) given in (2.37), compute \(E\left(u_{i, T+S} u_{i t}ight)\) for \(t=\) \(1,2, \ldots, T\) and verify that \(w=E\left(u_{i, T+S} uight)=\sigma_{\mu}^{2}\left(l_{i} \otimes \iota_{T}ight)\) where \(l_{i}\) is the \(i\) th column of \(I_{N}\).

(b) Verify (2.39) by showing that \(\left(l_{i}^{\prime} \otimes \iota_{T}^{\prime}ight) P=\left(l_{i}^{\prime} \otimes \iota_{T}^{\prime}ight)\).

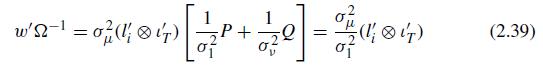
ViT+S = ZT+S8GLS +w'nuGLS for s> 1 (2.37)