Davison Electronics manufactures two LCD television monitors, identified as model A andmodel B. Each model has its lowest possible production cost when produced on Davison’s new production line. However, the new production line does not have the capacity to handle the total production of both models. As a result, at least some of the production must be routed to a higher-cost, old production line. The following table shows the minimum production requirements for next month, the production line capacities in units per month, and the production cost per unit for each production line:

Let
            AN = Units of model A produced on the new production line
            AO = Units of model A produced on the old production line
            BN = Units of model B produced on the new production line
            BO = Units of model B produced on the old production line

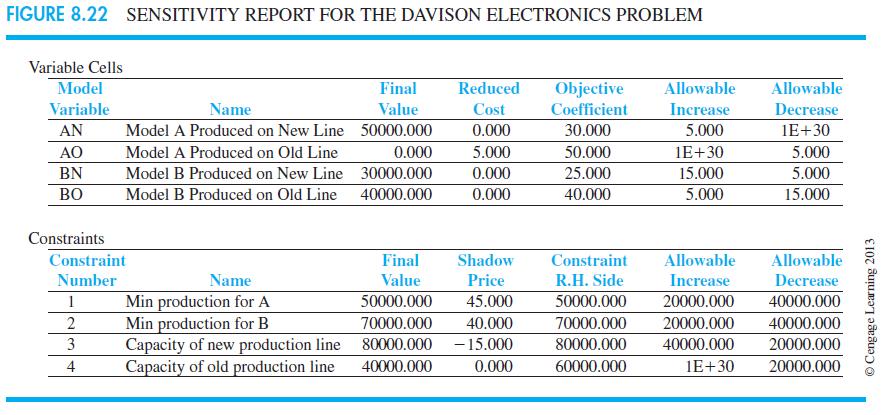
Davison’s objective is to determine the minimum cost production plan. The sensitivity report is shown in Figure 8.22.
  a. Formulate the linear programming model for this problem using the following four constraints:

    Constraint 1: Minimum production for model A

    Constraint 2: Minimum production for model B

    Constraint 3: Capacity of the new production line
    Constraint 4: Capacity of the old production line

  b. Using the sensitivity analysis information in Figure 8.22, what is the optimal solution and what is the total production cost associated with this solution?
  c. Which constraints are binding? Explain.
  d. The production manager noted that the only constraint with a negative shadow price is the constraint on the capacity of the new production line. The manager’s interpretation of the shadow price was that a one-unit increase in the right-hand side of this constraint would actually increase the total production cost by $15 per unit. Do you agree with this interpretation? Would an increase in capacity for the new production line be desirable? Explain.

  e. Would you recommend increasing the capacity of the old production line? Explain.
  f. The production cost for model A on the old production line is $50 per unit. How much would this cost have to change to make it worthwhile to produce model A on the old production line? Explain.
  g. Suppose that the minimum production requirement for model B is reduced from 70,000 units to 60,000 units. What effect would this change have on the total production cost? Explain.