(LMLE) Show that the LMLE will work with any initial estimator that is $\sqrt{N}$ consistent under the conditions of Lemma 15.7

(LMLE, p. 333).

*16.13 Suppose that $\{(x_n, y_n), n = 1, \dots, N\}$ are i.i.d. random variables and that the conditional distribution of $y_n$ given $x_n$ is $y|\mu(\beta_0; x_n), \sigma^2\}$, where $\mu(\beta_0; x_n)$ is a twice continuously differentiable function.

(a) Give sufficient conditions so that the NLS estimator $\hat{\beta}_{NLS}$ for $\beta_0$ is consistent.

(b) Give sufficient conditions so that

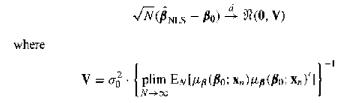
Explain how OLS is a special case.

(c) Give an estimator of the asymptotic variance of $\hat{\beta}_{NLS}$.

(d) Show that the asymptotic distribution of the NLS estimator is not changed by removing the normality assumption while retaining $E[y_n|x_n] = \mu(\beta_0; x_n)$ and $Var[y_n|x_n] = \sigma^2

where NBNIS -Bo)(0, V) Voplim Evita (Bo: Xn) g (B: Xx }' |