Carry out the integration details to develop the displacements (5.7.4) in Example 5.1. Equation 5.7.4 Data from
Question:
Carry out the integration details to develop the displacements (5.7.4) in Example 5.1.
Equation 5.7.4
![u= W = vpgxz E V = vpgyz E pg 21 [2 +v(x + y) 1]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/2/042659f80ea8d9691704952041578.jpg)
Data from example 5.1
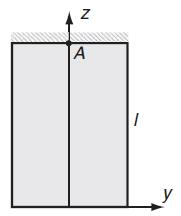
As an example of a simple direct integration problem, consider the case of a uniform prismatic bar stretched by its own weight, as shown in Fig. 5.11. The body forces for this problem are Fx = Fy = 0, Fz =–ρg, where ρ is the material mass density and g is the acceleration of gravity. Assuming that on each cross-section we have uniform tension produced by the weight of the lower portion of the bar, the stress field would take the form:
fig 5.11

This equation can be integrated directly, and applying the boundary condition σz = 0 at z = 0 gives the result σz(z) = ρgz. Next, by using Hooke’s law, the strains are easily calculated as:
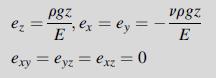
The displacements follow from integrating the strain-displacement relations (5.1.1), and for the case with boundary conditions of zero displacement and rotation at point A (x = y = 0, z = l), the final result is:
Equation 5.1.1
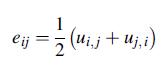
![-= n W = vpgxz E Pg 2E -=A vpgyz E = [2 +v(x + y) 1]](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1704/9/5/2/497659f82b133ca41704952496216.jpg)
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





