Using the inverse method, investigate which problem can be solved by the two-dimensional stress distribution x = Axy, xy = B + Cy

Using the inverse method, investigate which problem can be solved by the two-dimensional stress distribution σ_x = Axy, τ _xy = B + Cy², σ_y = 0, where A, B, and C are constants. First show that the proposed stress field (with zero body force) satisfies the stress formulation field equations under the condition that C =–A/2. Note that for this two-dimensional plane stress case, the Beltramie-Michell compatibility equations reduce to the form given by (7.2.7). Next choose a rectangular domain 0 ≤ x≤ l and –h ≤y ≤h, with l≫and investigate the interior and boundary stresses. Finally use strength of materials theory to show that these stresses could represent the solution to a cantilever beam under end loading. Explicitly determine the required constants A, B, and C to solve the beam problem.

Equation 7.2.7

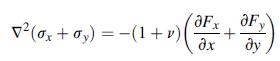
v(ox+ay) = -(1+0)( aFx aFy + dy