For the doublet mechanics Flamant solution in Example 15.15, develop contour plots (similar to Fig. 15.22) for the microstresses p₁ and p₂. Are there zones where these microstresses are tensile?

Data from example 15.15

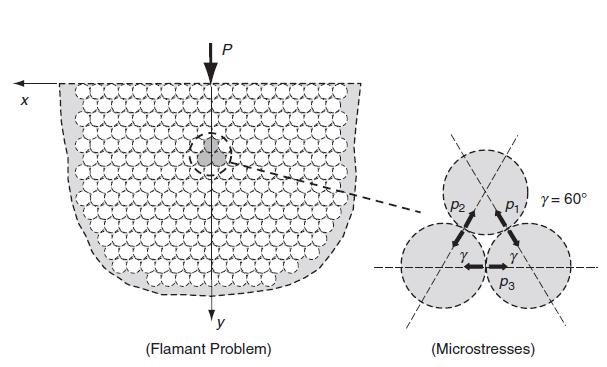
Fig 15.22

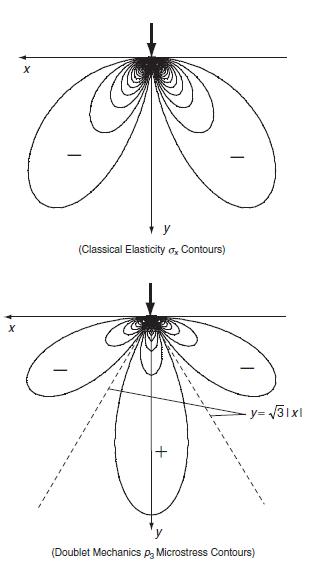
We now wish to investigate a specific application of the doublet mechanics model for a two- dimensional problem with regular particle packing microstructure. The case of interest is the Flamant problem of a concentrated force acting on the free surface of a semi-infinite solid, as shown in Fig. 15.21. The classical elasticity solution to this problem was originally developed in Section 8.4.7, and the Cartesian stress distribution was given by 0x = - dy Txy = 2Pxy (x + y) 2Py3 (x + y) 2Pxy (x +1) (15.6.9) This continuum mechanics solution specifies that the normal stresses are everywhere compressive in the half space, and a plot of the distribution of normal and shear stresses on a surface y constant was shown in Fig. 8.20. The doublet mechanics model of this problem is established by choosing a regular two- dimensional hexagonal packing, as shown in Fig. 15.21. This geometrical microstructure establishes three doublet axes at angles y = 60 as shown. Using only first-order approximation,