Question: Consider the gradient elasticity problem under a one-dimensional deformation field of the form u = u(x), v = w = 0. Using constitutive form (15.7.3),

Consider the gradient elasticity problem under a one-dimensional deformation field of the form u = u(x), v = w = 0. Using constitutive form (15.7.3), determine the stress components. Next show that equilibrium equations reduce to dσ_x/
dx = 0, and this will lead to the equation:

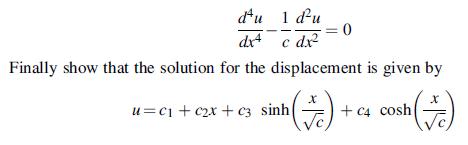
1 du c dx du dx4 Finally show that the solution for the displacement is given by h(c). ve) +c4 cosh(

Equation 15.7.3

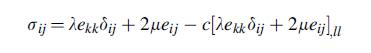
1 du c dx du dx4 Finally show that the solution for the displacement is given by h(c). e) + C4 cosh( u=c+c2x+c3 sinh = 0 X (JC)

Step by Step Solution

★★★★★

3.58 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

One dimensional displacement field u ux vw0 du Only one nonzero strain component e dx ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Elasticity Theory Applications Questions!

Carry out the integration details to develop the displacements (5.7.4) in Example 5.1. Equation 5.7.4 Data from example 5.1 As an example of a simple direct integration problem, consider the case of...

Under the stated symmetry conditions in Section 11.7.2, explicitly show that in the absence of body forces the general equilibrium equations reduce to forms (11.7.17) and (11.7.18). Verify the...

Consider the axisymmetric half-space problem shown in Fig. 14.19 for the case where only Poissons ratio is allowed to vary with depth coordinate v = v(z). Using cylindrical coordinates (r, , z) to...

Using integral tables verify that the gradient Flamant stress integral solution in Example 15.17 reduces to the classical elasticity form as per equations (15.7.20). Data from example 15.17 Equation...

3-(30%) Consider the following second order tensor F shown in its 2D component form: Later we will see that F is deformation gradient tensor defining a simple shear deformation shown in the Figure 1....

s1 educated (SSE) student for every three public school educated (PSE) students. Reasoning that students are not very dissimilar from threads, he suggests the following entry and exit routines be...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Please help! 3.4 Projectile Motion 27 .A ball is thrown horizontally from the top of a 60.0-m building and lands 100.0 m from the base of the building. Ignore air resistance. (a) How long is the ball...

(1) Consider a cylindrical bar of radius R and length L. The displacements are constrained by a frictionless rigid base at at x = 0. A uniform pressure P is applied at x = L and the other surfaces of...

(a) In SystemVerilog, what is the difference between: (i) The ternary operator ? and if...then...else statements? [2 marks] (ii) always_ff and always_comb? [2 marks] (iii) Blocking, non-blocking and...

Presented below is an aging schedule for Royal Company. Customer Total Not Yet Due Number of days past due 1-30 31-60 61-90 Over 90 Aber $20,000 $9,000 $11,000 Bohr 30,000 30,000 Case 50,000 15,000...

Calhoun/Johnson Company d/b/a Williams Lumber Company (Williams) sold building materials to Donald Miller d/b/a Millercraft Construction Company (Millercraft) on credit. Miller had signed a personal...

If the labor market shown in Exhibit 12 is a monopsony, the wage rate and number of workers employed will be determined at point a. A. b. W. c. C. d. Y. e. Z.

Which of the following is not a control activity? a. Proper authorization b. Security measures c. Risk assessment d. Mandatory vacations AppendixLO1

The following table shows the average temperature for each year in a certain city. Plot the data as a stem plot, a bar plot, and a stairs plot. Year 2000 2001 2002 2003 2004 Temperature (C) 21 18 19...

A sum of $10 000 invested at 4 percent interest compounded annually will grow according to the formula y(k) = 10 4 (1.04) k where k is the number of years (k = 0, 1, 2, . . .). Plot the amount of...

The volume V and surface area A of a sphere of radius r are given by a. Plot V and A versus r in two subplots, for 0.1 r 100 m. Choose axes that will result in straight-line graphs for both V and...

Use LINEST and the trend line equation to find your coefficient and its uncertainty. I hope this is enough information. The LINEST functions below the area correspond to the total mass/ average...

Melanie founded her company using $250,000 of her own money, issuing herself 100,000 shares of stock. An angel investor bought an additional 50 000 shares for $350000.shiw now sells another 190000...

( CPP ) This datatypes are derived from the primitive datatype