For the torsion of cylinders discussed in Section 11.4, show that with x = y
Question:
For the torsion of cylinders discussed in Section 11.4, show that with σx = σy = σz = τ xy = 0, the compatibility equations yield:
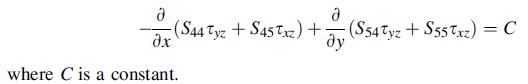
Data from section 11.4
As our first example, consider the torsion of a prismatic bar of arbitrary cross-section, as shown in Fig. 11.5. The isotropic problem was investigated in Chapter 9, and we now wish to formulate and develop solutions to the problem where the bar material is anisotropic with a plane of material symmetry normal to the bar axis (z-axis). For this case, the x,y-plane is the symmetry plane (similar to Fig. 11.2), and the elasticity matrix takes the reduced form for a monoclinic material as given by Eq. (11.2.7).
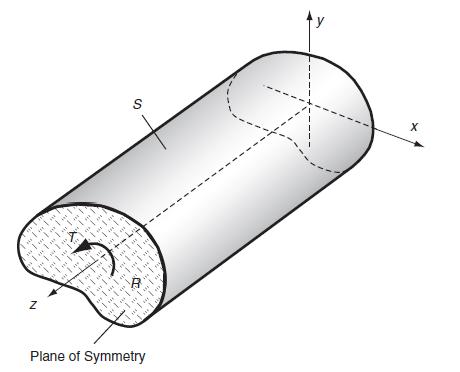
Following the usual procedure for torsion problems, boundary conditions are formulated on the
lateral surface S and on the end sections R. Conditions on the lateral surfaces of the bar are to be stress free, and these traction conditions are expressed as:
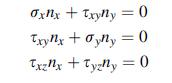
where nx and ny are the components of the unit normal vector to surface S. The loadings on the end sections (or any bar cross-section R) reduce to a single resultant moment T about the z axis, and this is formulated as:
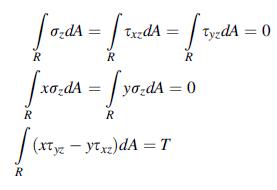
Step by Step Answer:

Elasticity Theory Applications And Numerics
ISBN: 9780128159873
4th Edition
Authors: Martin H. Sadd Ph.D.





