The plane stress solution for a semi-infinite elastic solid under a concentrated point loading is developed in Chapter 8. With respect to the axes shown in the following figure, the Cartesian stress components are found to be:

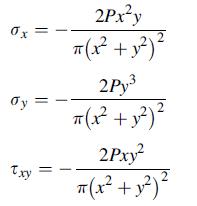
Using results from Exercise 3.5, calculate the maximum shear stress at any point in the body and plot contours of τ _max. You can compare your results with the corresponding photo elastic contours shown in Fig. 8.28. Example MATLAB Code C-3 will be useful to develop the contour plotting code.

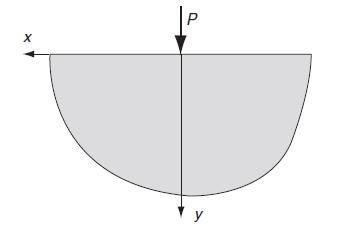
Data from exercise 3.5

A two-dimensional state of plane stress in the x, y-plane is defined by σ_z = τ _yz = τ _zx = 0. Using general principal value theory, show that for this case the in-plane principal stresses and maximum shear stress are given by:

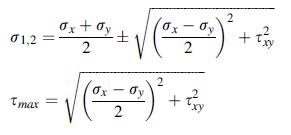
Fig 8.28

Ox Txy 2Pxy (x + y) 2 2Py (x + y) 2 2Pxy (x + y) 2