Using the solution from Example 10.7, apply the principle of superposition and solve the problem of a stress-free elliptical hole under uniform biaxial tension as shown. In particular show that the circumferential stress is given by:

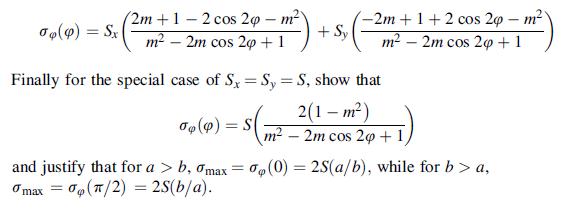
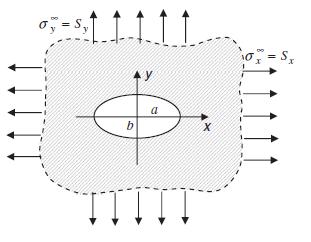
Data from example 10.7

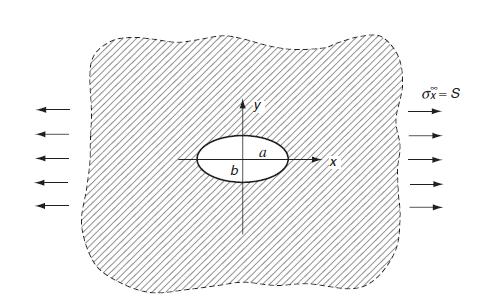
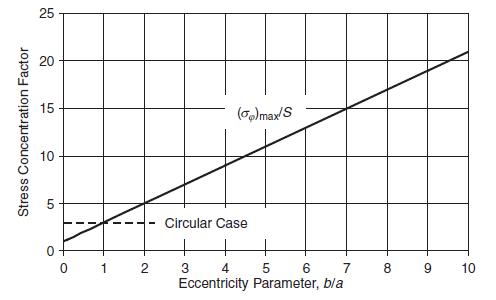
Jp (9) = Sx (2m+1-2 cos 2p - m m 2m cos 20+1 Finally for the special To (9)= S( case of Sx = Sy = S, show that 2(1-) 2m cos 2p+1, = and justify that for a> b, max: max = 0,(1/2) = 25(b/a). m + Sy - -2m+1+2 cos 2q - m m - 2m cos 2p+1 op (0)= 2S(a/b), while for b> a,