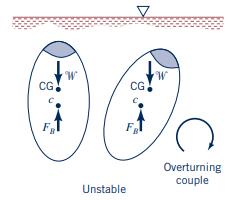
As shown in Fig. 2.26. Fig. P7.41, a rectangular barge floats in a stable configuration provided the distance between the center of gravity, \(C G\), of the object (boat and load) and the center of buoyancy, \(C\), is less than a certain amount, \(H\). If this distance is greater than \(H\), the boat will tip over. Assume \(H\) is a function of the boat's width, \(b\), length, \(\ell\), and draft, \(h\).

(a) Put this relationship into dimensionless form.

(b) The results of a set of experiments with a model barge with a width of \(1.0 \mathrm{~m}\) are shown in the table. Plot these data in dimensionless form and determine a power-law equation relating the dimensionless parameters.

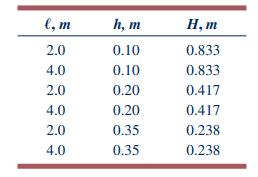
Figure P7.41

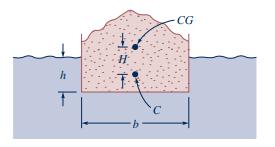
Fig. 2.26

l, m h, m H, m 2.0 0.10 0.833. 4.0 0.10 0.833 2.0 0.20 0.417 4.0 0.20 0.417 2.0 0.35 0.238 4.0 0.35 0.238