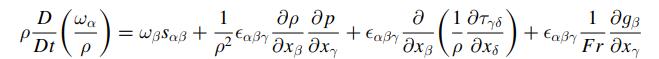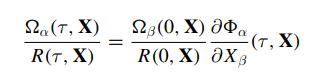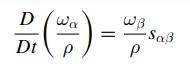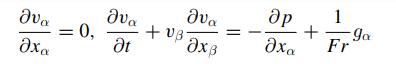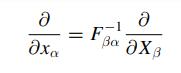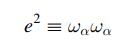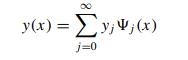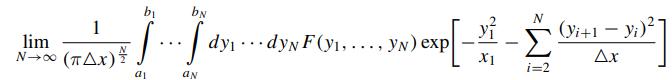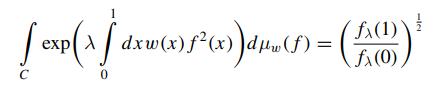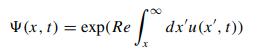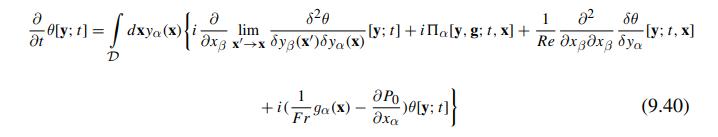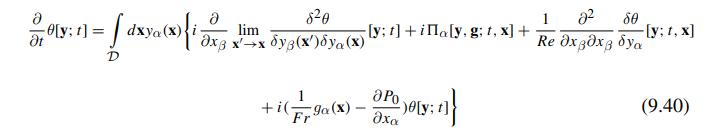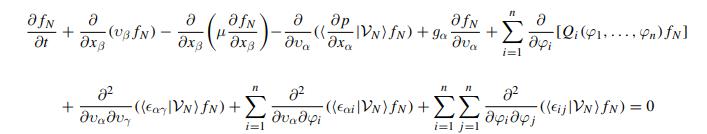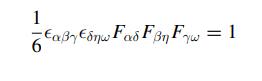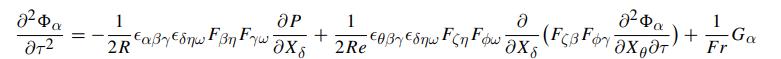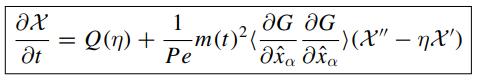Navier Stokes Turbulence Theory And Analysis 1st Edition Wolfgang Kollmann - Solutions

Discover the ultimate resource for tackling complex problems with the "Navier Stokes Turbulence Theory And Analysis" textbook by Wolfgang Kollmann. Access our comprehensive online solutions manual and answers key, offering step-by-step answers and solved problems to enhance your understanding. Utilize our free download solutions PDF and test bank for detailed chapter solutions and instructor manual insights. Perfect for students and educators alike, our guide provides essential questions and answers to navigate the intricacies of turbulence theory. Unlock the full potential of your studies with our expertly crafted content, ensuring success in mastering this complex subject.

Derive the dimensional vorticity pde (2.62) for a single, compressible Newtonian fluid using Cartesian coordinates.pde (2.62) 1 D Wa = wsa + 5 EaY 1 + Eay + Eay 1 Fr ax Dt
Verify that (2.69) is the solution of the vorticity pde (2.65) in \(\mathcal{D}=R^{3}\) for inviscid and barotropic fluids.pde (2.69)pde (2.65) (T, X) R(T, X) (0, X) a (T, X) R(0, X) OXB
Consider the flow of an inviscid, incompressible fluid with non-zero vorticity governed by the Euler pdes in \(\mathcal{D}=R^{3}\), let the vorticity be specified initially as a smooth vector field \(\Omega_{\alpha}(0, \mathbf{X}) \in L_{\mathcal{D}}^{2}\), then establish the equation for the
Consider the flow of an incompressible, Newtonian fluid. Define the Lamb vector by Eq. (2.54) \(\mathbf{L} \equiv \omega \times \mathbf{v}\), where \(\boldsymbol{\omega} \equiv abla \times \mathbf{v}\) denotes the vorticity vector.2.4.1 Show that the convective acceleration is the sum of the Lamb
Determine the symmetries of the heat pde\[ \frac{\partial T}{\partial t}-\frac{\partial^{2} T}{\partial x^{2}}=0 \]defined on \(\mathcal{D}=[0, \infty] \times R^{1}\).2.5.1 Change the notation to \(x \rightarrow x_{1}, t \rightarrow x_{2}, T \rightarrow y_{1}\) and determine the prolonged
Integrate the Euler pdes (2.9)\[ \begin{gathered} \frac{\partial v_{\alpha}}{\partial x_{\alpha}}=0 \\ \frac{\partial v_{\alpha}}{\partial t}+v_{\beta} \frac{\partial v_{\alpha}}{\partial x_{\beta}}=-\frac{\partial p}{\partial x_{\alpha}} \end{gathered} \]governing the motion of an
Derive the pde for the dimensionless mean kinetic energy \(k \equiv \frac{1}{2}\left\langle v_{\alpha}^{\prime} v_{\alpha}^{\prime}\rightangle\) assuming a viscous, incompressible Newtonian fluid. Identify production, viscous destruction and the total turbulent flux terms.
Derive the pde for the dimensionless mean enstrophy \(\left\langle e^{2}\rightangle\) defined by (3.16) in homogeneous turbulence for an incompressible Newtonian fluid with constant viscosity \(\tilde{u}>0\), i.e. \(0 Eq (3.16) e
Consider the pde for the mean enstrophy obtained in the previous problem.(3.3.1) Solve the pde assuming that the vortex stretching term has the form\[ \left\langle\omega_{\alpha} \omega_{\beta} \frac{\partial v_{\alpha}}{\partial x_{\beta}}\rightangle \approx A e^{\frac{3}{2}} \]where \(A>0\) is
The Jacobi orthogonal polynomials \(P_{n}^{\alpha, \beta}(x)\), which are the solutions of the ode\[ \left(1-x^{2}\right) \frac{d^{2} P_{n}^{\alpha, \beta}}{d x^{2}}+[\beta-\alpha-(\alpha+\beta+2) x] \frac{d P_{n}^{\alpha, \beta}}{d x}+n(n+\alpha+\beta+1) P_{n}^{\alpha, \beta}=0 \]are related to
The Hermite functions (Sect. 4.3.3) are a basis for the space \(\Omega=\) \(C_{R^{1}}^{\infty} \cap L_{R^{1}}^{2}\) of functions defined on the unbounded domain \(R^{1}\). Determine the coordinates \(c_{i}\) with respect to the basis \(\left\{\Psi_{n}(x): n=0,1, \ldots, \infty\right\}\) of the test
Solve the BVPs for the Poisson pdes\[ \epsilon_{\delta \eta \alpha} \frac{\partial \omega_{\alpha}}{\partial x_{\eta}}=\frac{\partial^{2} v_{\eta}}{\partial x_{\delta} \partial x_{\eta}}-\frac{\partial^{2} v_{\delta}}{\partial x_{\eta} \partial x_{\eta}} \]or in symbolic notation\[ abla \times
Let \(\Omega=\left\{\mathbf{v}(\mathbf{x}) \in L_{\mathcal{D}}^{2} \cap C_{\mathcal{D}}^{2}\right\}\) be the phase space for the compact flow domain \(\mathcal{D} \subset R^{3}\) with n.e. smooth boundary \(\partial \mathcal{D}, \Omega\) is then Hilbert space w.r.t.\[
Compute the Wiener integral of the functional\[ \begin{equation*} F[f(x)]=\exp \left\{\lambda \int_{0}^{1} d y w(y) f^{2}(y)\right\} \tag{6.42} \end{equation*} \]directly (without using the Cameron-Martin theorems), where \(\lambda\) is a real number and \(w(x)>0, x \in[0,1]\), over the space
Compute the Wiener integral (6.39) for \(p(x)=1, q(x)=0\) and \(w(x)=(x+\alpha)^{-2}\), where \(0Eq (6.39) [ exp(x dxw(x) f(x) ditu (f) = (()) C 0 dw
Consider the space of continuous functions \(C=\{f(x), x \in[0,1]\}\) defined on the domain \(\mathcal{D}=[0,1]\). Solve the IVP for the functional differential equation\[ \frac{\delta F[f]}{\delta f(x)}=b(x) f(x)^{n} F[f] \]where \(n>0\) is integer, for the functional \(F[f]: C \rightarrow R^{1}\).
Consider the space of twice continuously differentiable functions \(C^{2}=\{f(x), x \in[0,1]\}\). Solve the functional differential equation\[\frac{\delta F[f]}{\delta f(x)}=\left[-\frac{d^{2} f}{d x^{2}}+c f(x)+g f^{3}(x)\right] F[f]\]where \(c, g\) are constants, for the functional \(F[f]: C
Solve the pure IVP for the Burgers pde (1.2) with initial condition \(u(0, x)=u_{0}(x) \in L_{\mathcal{D}}^{2} \cap C_{\mathcal{D}}^{\infty}, \mathcal{D}=(-\infty, \infty)\), using the Hopf-Cole transformation (1.3).Pde (1.2)Eq (1.3) + || | 1 2Re 3
Derive the Hopf fde for the characteristic functional \(\theta[y ; t]\) for the pure IVP of the Burgers pde (1.2). Use the result obtained in Problem (9.1) to establish the solution operator and its inverse.Problem 9.1Solve the pure IVP for the Burgers pde (1.2) with initial condition \(u(0,
Solve the Hopf fde for the Burgers pde using the solution operator established in Problem (9.2). The initial condition is the characteristic functional \(\theta[y ; 0]\) for Gaussian stochastic fields with zero mean.9.3.1: Specify the initial condition for Gaussian random fields in terms of the
Consider an analytic functional \(R[y]\) defined on the phase space \(\Omega=\) \(\left\{y(\mathbf{x}) \in L_{R^{3}}^{2}\right\}, \mathbf{x} \in R^{3}\) and Gaussian stochastic fields \(f_{i}(t, \mathbf{x})\) with zero mean and positive definite correlation tensor defined by\[ K_{i, j}\left(t,
Solve the fde for the characteristic functional \(\theta[\mathbf{y}() ; t\).\[ \frac{\partial}{\partial t} \theta[\mathbf{y} ; t]=i \int_{\mathcal{D}} d \mathbf{x} y_{\alpha}(\mathbf{x})\left(\frac{1}{F r} g_{\alpha}(\mathbf{x})-\frac{\partial P_{0}}{\partial x_{\alpha}}\right) \theta[\mathbf{y} ;
Transform the Hopf fde (9.40) to cylindrical coordinates in \(\mathcal{D}\). The explicit form of the pressure gradient term as functional of the velocity is not required. 1 82 80 [y; t]+illaly, g; t, x]+ [y; 1, x] Re Ox30x8 Sya t] dxya(x) lim 820 () 0[y; 1] = [ dxya (x) {i x x x 5y3(x)ya (x) \
Apply the conditions of steady state and solenoidal vector fields \(\mathbf{y}\) to the Hopf fde for cylindrical coordinates in the flow domain \(\mathcal{D}\) obtained in the previous Problem (10.2).10.3.1 Specialize the result to constant \(\mathbf{G}\) and \(\frac{\partial P_{0}}{\partial
Consider the flow through a straight, circular pipe periodic in axial direction. A solenoidal ONS basis \(\mathcal{B}_{e}\) was constructed in Sect. 25.21 spanning the test function space \(\mathcal{N}\) for the characteristic functional \(\theta[\mathbf{y} ; t], \mathbf{y} \in \mathcal{N}\). Solve
A random variable \(Y(t)\) defined on \(R^{1}\) is specified by the Pdf\[ f_{Y}(t)=\frac{1}{2} \exp (-|t|) \]Compute the characteristic function \(\theta(\zeta)\) and all statistical moments using \(\theta\).
Consider the random variable \(\epsilon>0\) such that\[ \Phi=\ln \left(\frac{\epsilon}{\epsilon_{0}}\right) \]is Gaussian with mean \(\langle\Phiangle\) and variance \(0
Consider the dynamics of a passive scalar \(0 \leq \Phi(t, \mathbf{x}) \leq 1\) in a turbulent flow. Specialize the transport pde (11.52) for the \(\operatorname{Pdf} f_{N}\left(\varphi_{1}, \ldots, \varphi_{N}\right)\) of \(N\) scalars to the Pdf \(f(\varphi)\) for a single scalar \(\Phi\) and
Compute the Gateaux derivative with respect to \(v_{\alpha}(\mathbf{x}, t)\) of the pressure represented in terms of the Green's function as shown in Sect. 11.1 for nonhomogeneous Neumann conditions for the pressure and homogeneous Dirichlet boundary conditions for the momentum balances. Specialize
The initial value problem (IVP) for the ode\[ \frac{d Y}{d t}=-C Y^{2} \]with \(C\) being a positive constant and initial condition \(Y(0)=Y_{0} \geq 0\) generates a mapping \(Y(t): Y(0) \rightarrow R^{1}\).12.1.1 Compute the solution of the IVP.12.1.2 Let the initial value \(Y_{0}\) be a random
Derive the single label Pdf equation for position \(\Phi_{\alpha}(\tau, \mathbf{X})\) in the material description. Use the coarse-grained Pdf\[ \hat{f} \equiv \prod_{\alpha=1}^{3} \delta\left(\Phi_{\alpha}(\tau, \mathbf{X})-q_{\alpha}\right) \]and the Navier-Stokes pdes (2.85), (2.86) in the
Compute the analytic solution of the IVP for the mapping pde (13.23) for a single conserved \((Q(\eta)=0)\) scalar. The scalar space is the unit interval \(\mathcal{R}_{\Phi}=\) \([0,1]\), and the initial condition is\[ \mathcal{X}(\eta ; 0)=\sum_{k=1}^{N} w_{k} H\left(\eta-\eta_{k}\right), w_{k}
Compute and plot the Jacobian \(J(\eta ; t)\) and the \(\operatorname{Pdf} f(\varphi ; t)\) for \(t>0\) using the mapping \(\mathcal{X}(\eta ; t)\) of the previous problem 13.1.Problem 13.1Compute the analytic solution of the IVP for the mapping pde (13.23) for a single conserved \((Q(\eta)=0)\)
Consider the discriminating scalar \(\Phi(t, \mathbf{x}) \geq 0\) governed by\[ \frac{\partial \Phi}{\partial t}+v_{\alpha} \frac{\partial \Phi}{\partial x_{\alpha}}=\frac{\partial}{\partial x_{\alpha}} \frac{1}{\operatorname{ScRe}} \frac{\partial \Phi}{\partial x_{\alpha}}+Q(\Phi) \]where \(S c\)
Compute the intermittency generating vector (16.19)\[ \varphi_{\alpha}(\mathbf{w} ; \tau, \Delta \tau, \mathbf{X})=\frac{1}{\sqrt{\Sigma_{(\alpha \alpha)}}}\left\langle\Delta A_{\alpha} \mid \mathbf{W}=\mathbf{w}\rightangle-w_{\alpha}\left(\left\langle\triangle A_{(\alpha)}
Consider stationary and locally isotropic turbulence at high Renumber. A simple model for the energy spectrum can be constructed by defining a sequence of wavenumbers \(k_{n}\), such that\[ k_{n+1}=2 k_{n} \]Let the energy contained in the interval \(\left[k_{n}, k_{n+1}\right]\) be \(E(k)\) and
Determine the pde for helicity density \(h(t, \mathbf{x}) \equiv \mathbf{v} \cdot !\) for the flow of an incompressible Newtonian fluid. Define helicity \(\mathcal{H}\) by (15.30) and establish the equation for it.Eq (15.30) H = dv(x)h(x) D
Compute the solution \(\Psi\) of the pde (20.26) for the Chaplygin-Lamb dipole streamfunction\[ \frac{\partial^{2} \Psi}{\partial r^{2}}+\frac{1}{r} \frac{\partial \Psi}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} \Psi}{\partial \theta^{2}}=-\omega \]for \(\omega(r, \theta)=n^{2} \Psi(r,
Compute the solution \(\Psi\) of the pde (20.26) for the Chaplygin-Lamb dipole streamfunction\[ \frac{\partial^{2} \Psi}{\partial r^{2}}+\frac{1}{r} \frac{\partial \Psi}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2} \Psi}{\partial \theta^{2}}=-\omega \]for \(\omega(r, \theta)=n^{2}(\Psi(r,
Determine the material deformation gradient as measured by deformation gradient and deformation rate (velocity gradient) for the restricted Euler system. The restricted Euler flow is governed by (2.122) introduced in Sect. 2.7.(4.1) Derive the pde for the deformation gradient \(F_{\alpha \beta}\)
One of many Lagrangean line structures in turbulent flows is considered in elementary form. The example, called Shilnikov system, is constructed as simplified velocity field that contains several critical points. The solution of the autonomous Shilnikov system [74, 75] for the Lagrangean position
Townsend's model eddy (19.1) is a localized blob of vorticity defined in \(\mathcal{D}=R^{3}\) (Davidson [76], Sect. 6.4.1, cylindrical coordinates) by \(v_{r}=v_{z}=0\) and\[ v_{\theta}=\Omega r \exp \left(-2 \frac{\mathbf{x} \cdot \mathbf{x}}{z_{c}^{2}}\right) \]where \(z_{c}>0\) denotes the
Consider the fully developed, turbulent flow of an incompressible, Newtonian fluid through a plane channel between two plates at \(x_{2}=0\) and \(x_{2}=h\). Use dimensionless variables based on the kinematic viscosity \(u\) and the wall shear velocity \(u_{\tau}\) (27.15).1.1 Derive the averaged
Consider a materially invariant admissible circuit \(\mathcal{C}\), as defined in Sect. 2.6.3, embedded in a flow field \(\mathcal{D}\). The incompressible fluid is in turbulent motion governed by the Navier-Stokes pdes. Assume that appropriate reference values exist and the Reynolds number \(R e
Orlandi and Carnevale [37] argue that the nonlinear amplification of vorticity in inviscid interaction is a candidate for the appearance of a finite-time singularity of the second kind starting from smooth initial data, check Eq. (3.15) in Chap. 3 for definition. The ode\[ \frac{\partial
Show that the Duchon-Robert smoothness term \(D(\mathbf{v})\) in Sect. 22.3 is zero for the following class of velocity fields \(\mathbf{v}(\mathbf{x}, t)\) :\[ \int_{\mathcal{D}} d \mathbf{w}|\mathbf{v}(\mathbf{x}+\mathbf{w}, t)-\mathbf{v}(\mathbf{x}, t)|^{3} \leq C(t)|\mathbf{w}|

Navier Stokes Turbulence Theory And Analysis 1st Edition Wolfgang Kollmann - Solutions

Step by Step Answers