Compute and plot the Jacobian (J(eta ; t)) and the (operatorname{Pdf} f(varphi ; t)) for (t>0) using
Question:
Compute and plot the Jacobian \(J(\eta ; t)\) and the \(\operatorname{Pdf} f(\varphi ; t)\) for \(t>0\) using the mapping \(\mathcal{X}(\eta ; t)\) of the previous problem 13.1.
Problem 13.1
Compute the analytic solution of the IVP for the mapping pde (13.23) for a single conserved \((Q(\eta)=0)\) scalar. The scalar space is the unit interval \(\mathcal{R}_{\Phi}=\) \([0,1]\), and the initial condition is
\[ \mathcal{X}(\eta ; 0)=\sum_{k=1}^{N} w_{k} H\left(\eta-\eta_{k}\right), w_{k} \geq 0, \sum_{k=1}^{N} w_{k}=1 \]
where \(H\left(\eta-\eta_{k}\right)\) denotes the unit step function located at \(\eta_{k}\).
13.1.1: Rescale the time variable \(t\) to transform the mapping pde to the form
\[ \left(\frac{\partial}{\partial \tau}+\eta \frac{\partial}{\partial \eta}-\frac{\partial^{2}}{\partial \eta^{2}}\right) \mathcal{X}(\eta, \tau)=0 \]
13.1.2: Transform the scalar variable using \(\tilde{\eta} \equiv \eta \exp (-\tau)\) to obtain a new pde for \(\mathcal{X}\).
13.1.3: Solve the new pde for \(\mathcal{X}\). The Green's function approach is recommended, see Duffy [9], Sect. 4.1 for details.
13.1.4: Plot the solution \(\mathcal{X}(\eta ; t)\) for several times in [0, 0.3].
pde (13.23)
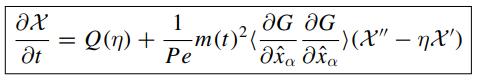
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann




