Compute the Wiener integral of the functional [ begin{equation*} F[f(x)]=exp left{lambda int_{0}^{1} d y w(y) f^{2}(y) ight}
Question:
Compute the Wiener integral of the functional
\[ \begin{equation*} F[f(x)]=\exp \left\{\lambda \int_{0}^{1} d y w(y) f^{2}(y)\right\} \tag{6.42} \end{equation*} \]
directly (without using the Cameron-Martin theorems), where \(\lambda\) is a real number and \(w(x)>0, x \in[0,1]\), over the space \(C_{0}\) of continuous functions \(f(x), x \in[0,1]\) with respect to the Wiener measure.
6.1.1 Use the definition of the Wiener integral (6.31) and the relation
\[ \begin{equation*} \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} d x_{1} \cdots d x_{N} \exp \left(-\sum_{i=1}^{N} \sum_{j=1}^{N} a_{i, j} x_{i} x_{j}\right)=\pi^{\frac{N}{2}}\left[\operatorname{det}\left(a_{i, j}\right)\right]^{-\frac{1}{2}} \tag{6.43} \end{equation*} \]
valid for positive definite matrices \(a_{i, j}\) to derive a recursive relation for the determinant of \(a_{i, j}\). Establish the ode and the boundary conditions for \(N \rightarrow \infty\).
6.1.2 Solve the ode for \(w(x)=1\), compute the value of the functional integral and plot it as function of \(\lambda\).
Eq (6.31)
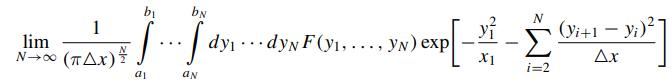
Step by Step Answer:

Navier Stokes Turbulence Theory And Analysis
ISBN: 9783030318697
1st Edition
Authors: Wolfgang Kollmann




