Consider a simple lottery based on the flip of a fair coin: If it lands tails, we win \(€ 10\), otherwise we lose \(€ 5\). Should we play this lottery? The expected payoff is \(€ 2.5\), and most people answer that they would be willing to take the gamble. If we spice things up and scale the payoff by a factor of one million, the answer turns probably negative. Sure, an expected payoff of \(€ 2.5\) million is quite palatable, but the considerable risk of losing \(€ 5\) million makes the gamble not attractive to most people.

However, imagine playing the gamble repeatedly many times, say, one thousand times. Our answer could change if we are allowed to settle the score at the end of the game. Let \(X_{i}\) be the payoff of flip number 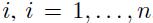, where \(n\) is the number of independent and identically distributed flips. Thus, the variables \(X_{i}\) are i.i.d. random variables.  be the total payoff, and let us denote the common expected value and standard deviation of the variables \(X_{i}\) by 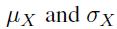, respectively. Then, the coefficient of variation of \(Y\), under the hypothesis of independent flips, is

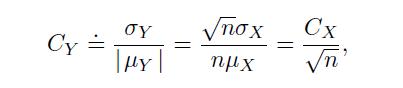
where we assume If \(n\) is large, the expected overall payoff becomes virtually certain (this is an informal glimpse of the law of large numbers). However, if we may go bankrupt along the way (i.e., we settle each flip of the coin individually, rather than assessing the overall profit/loss at the end of the game) or risks are correlated, this is not true anymore.

Transcribed Image Text:

i, i = 1,...,n