Say that we own a piece of real estate and we want to insure it against a disaster that may occur with probability \(p\). If disaster strikes, our loss is \(100 \%\) of the property value. Risk may be represented by a Bernoulli random variable:

- With probability \(p\), return is 1 (we lose \(100 \%\) of the property).

- With probability 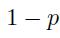, return is 0 .

Then,

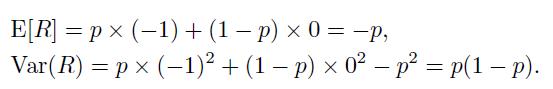
Note that the expected return is negative, as we are facing a potential loss. By abusing proper quadratic utility a little bit, let us consider the mean-risk form of Eq. (7.18),

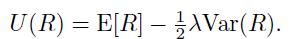
In this specific case, the utility score is, for a given risk aversion coefficient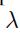

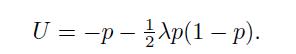
We may consider insuring the property for a given premium. The more we are willing to pay, the more risk-averse we are. If we are willing to pay at most , then the utility of the certain equivalent loss of is equal to the above utility score:

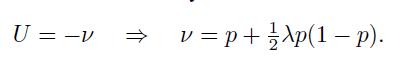
As a reality check, observe that a risk-neutral investor \((=0)\) would just pay \(p\), the expected loss. Given the insurance premium that we are willing to pay, this relationship allows to figure out a sensible value of 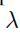, since

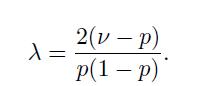
To get a more intuitive feeling, imagine that \(p\) is small (1 \(\quad p \quad 1\), so that

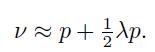
Let us try a few values of  :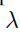

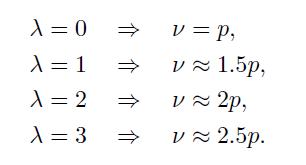
Therefore, for each unit increment in the risk aversion coefficient, we should be willing to pay another \(50 \%\) of the expected loss.
In portfolio optimization, it is commonly agreed that ranges between 2 and 4.

Data From Equation (7.18)

Transcribed Image Text:

1-p