Question: A classical problem in the calculus of variations is to find the shape of a curve C such that a bead, under the influence of

A classical problem in the calculus of variations is to find the shape of a curve C such that a bead, under the influence of gravity, will slide from point A(0, 0) to point B(x₁, y₁) in the least time. See the following figure. It can be shown that a nonlinear differential for the shape y(x) of the path is y[1 + (y')²] = k, where k is a constant. First solve for dx in terms of y and dy, and then use the substitution y = k sin²Î¸ to obtain a parametric form of the solution. The curve turns out to be a cycloid.

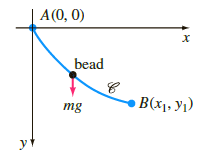
A(0, 0) х bead B(x1, y1) mg y+

A(0, 0) bead B(x1, y1) mg y+

Step by Step Solution

★★★★★

3.41 Rating (170 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Given y1 ydot 2 k now ydot dydx dydx 2 ky 1 therefore dx 2 dy 2 y k y this is the re... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (2 attachments)

1596_6062c74d05119_676500.pdf

180 KBs PDF File

1596_6062c74d05119_676500.docx

120 KBs Word File

Students Have Also Explored These Related First Course Differential Equations Questions!

Let a0, a1, . . . , an be n + 1 distinct real numbers. Define polynomials p0(x), p1 (x), . . . , Pn(x) by These are called the Lagrange polynomials associated with a0, a1, . . . , an [Joseph-Louis...

Calculus Kernels The transformations in Problems 1 to 3 should be familiar from calculus. Identify each transformation and give its kernel. 1. T: P2 P2. T(at2 + bt + c) = 2at + b 2. T: P2 P2. T(at2...

(Calculus Required) Let V be the vector space of continuous functions with basis {sint, cos t}, and let L: V V be defined as L(g(t)) = g'(t). Is L diagonalizable?

This example is valuable in emphasizing the restrictions that surround the derivation and the meaning of the stationary condition. Exercises 7 and 8 exam- ine the conditions for the pathological...

SUMMARY this article for about 2 pages with single spacing. Thank you. ECONOMETRICS: MEASUREMENT I N ECONOMICS1 I As the first incumbent of a new Chair in this University, I thought that in this...

Imagine a rigid metal wire, that is in the shape of a curve to be determined, going from the point ( 0 , 1 ) to the point ( 1 , 0 ) . A bead with a hole through it is placed on the wire at ( 0 , 1 )...

3. In your own words explain the two challenges and two opportunities in this case. (6 marks) Munich Re was keen to develop multiple digital offerings simultaneously. The company noticed, after...

Please do all letters Consider classical and quantum harmonic oscillators. When the classical harmonic oscillator is in the ground state, i.e., at rest, it sits still at the equilibrium position....

Pulang Malaysia Anda menguruskan sebuah syarikat percetakan dan telah menerima pesanan untuk mencetak brosur yang mengandungi peta Malaysia. Pelanggan telah meminta agar peta tersebut dicetak seperti...

1. (30 pts) Here is a classical problem that is often part of interviews. You are given n nuts and n bolts, such that one and only one nut fits each bolt. Your only means of comparing these nuts and...

Required: 1. On January 1, 20x5, JV purchased 1,000 of its own common shares for $23 each. Use the cost method. 2. On March 1, 20x5, JV reissued 500 of the shares acquired on January 1 at $33. 3. On...

What is the Austrian response to the hypothesis of the existence of a so-called savings glut, i.e. a situation of excess savings? a. A serious problem that only the market can solve b. A problem that...

A monopolist sets a. the highest possible price. b. a price corresponding to the minimum average total cost. c. a price equal to marginal revenue. d. a price determined by the point on the demand...

The ability of firms to enter and exit a market over time means that, in the long run, a. the demand curve is more elastic. b. the demand curve is less elastic. c. the supply curve is more elastic....

At teradatauniversitynetwork.com, read and answer the questions of the assignment Data Warehousing Failures. Because eight cases are described in that assignment, the class may be divided into eight...

Highlight the utility of the three types of metadata emphasized in the chapter.

Through customer service, resource optimization, and the innovative use of information and technology, the Michigan Department of Technology, Management & Budget (DTMB) impacts every area of...

Orange Corporation has just made a French Euro bid on a project located in France. It won't find out for 90 days whether it has won the contract. There will be a 15% signing bonus payable to the...

Consider the following table: Stock Fund Bond Fund Scenario Probability Rate of Return Rate of Return Severe recession 0.10 34% 10% Mild recession 0.20 18% 6% Normal growth 0.45 14% 7% Boom 0.25 24%...