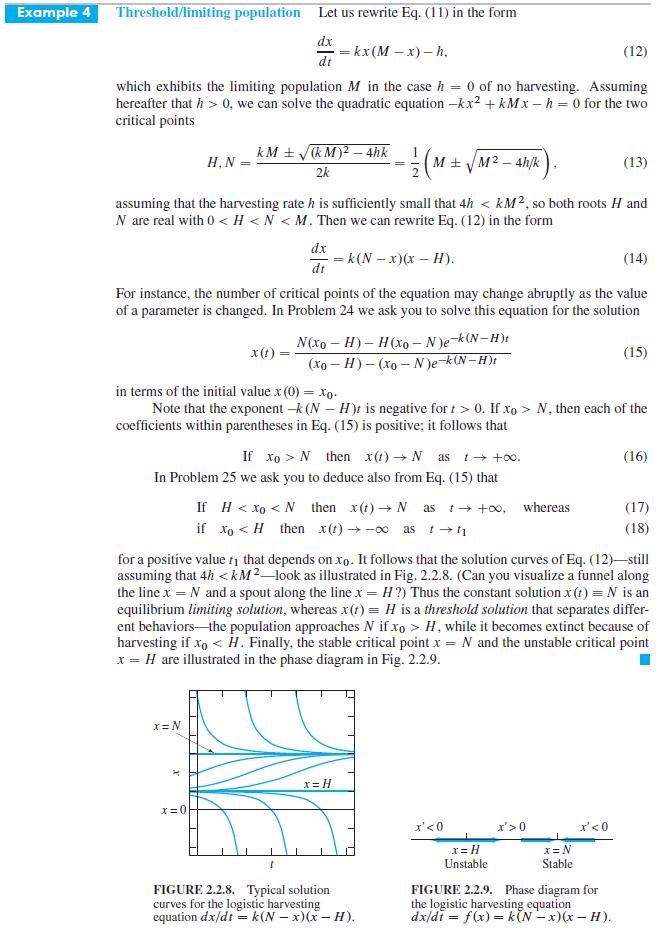
Example 4 dealt with the case 4h > kM² in the equation dx/dt = kx (M - x) - h that describes constant-rate harvesting of a logistic population. Problems 26 and 27 deal with the other cases.

If 4h = kM², show that typical solution curves look as illustrated in Fig. 2.2.14. Thus if x₀ ≧ M/2, then x (t) → M/2 as t →+ ∞. But if x₀ < M/2, then x (t) = 0 after a finite period of time, so the lake is fished out. The critical point x = M/2 might be called semistable, because it looks stable from one side, unstable from the other.

Transcribed Image Text:

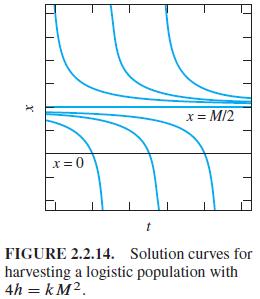
X x=0 t x = M/2 FIGURE 2.2.14. Solution curves for harvesting a logistic population with 4h = KM².