Question: The differential equation dx/dt = 1/10x(10 -x) - h models a logistic population with harvesting at rate h. Determine (as in Example 6) the dependence

The differential equation dx/dt = 1/10x(10 -x) - h models a logistic population with harvesting at rate h. Determine (as in Example 6) the dependence of the number of critical points on the parameter h, and then construct a bifurcation diagram like Fig. 2.2.12.

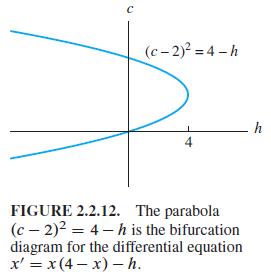
C (c-2) =4-h 4 FIGURE 2.2.12. The parabola (c-2) = 4-h is

C (c-2) =4-h 4 FIGURE 2.2.12. The parabola (c-2) = 4-h is the bifurcation diagram for the differential equation x' = x(4-x) - h. h

Step by Step Solution

★★★★★

3.44 Rating (154 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

The critical points of the given differential equa... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related First Course Differential Equations Questions!

What are the potential disadvantages of using bar raisers for Amazon? What are the potential advantages and disadvantages of bar raisers for job applicants of bar raisers being used?

The differential equation dx/dt = 1/100x(x - 5) + s models a population with stocking at rate s. Determine the dependence of the number of critical points c on the parameter s, and then construct the...

Example 4 dealt with the case 4h > kM 2 in the equation dx/dt = kx (M - x) - h that describes constant-rate harvesting of a logistic population. Problems 26 and 27 deal with the other cases. If 4h >...

The differential equation dp/dt= (1/2)P(3-P)-H models a logistic population with harvesting at rate H. Determine the dependence of the number of equilibria on the parameter H, and draw a bifurcation...

dx 1 The differential equation dt 14x(14-x)-h models a logistic population with harvesting at rate h. Determine the dependence of the number of critical points on the parameter h, and then construct...

Please answer all questions of Part E. Background You are a consultant who has been hired to help the province of Nova Scotia establish regulations for commercial cod fishing in their territorial...

Section 7.2 Reading Assignment: Exponential Change and Separable Differential Equations Answer Only Exercise 1, 2, and 3 by using a screenshot provided Calculus Pearson textbook. Make sure you read...

Investors need to be aware of nine sources of risk when calculating the riskreturn trade-off. List and briefly describe these nine sources of risk.

Refer to the audit report for Asyst Technologies in exhibit. The report is presented as an example of an adverse opinion on ICFR. Answer the following questions regarding the other contents of the...