Problems 20 through 22 deal with the case ∈ = -1, for which the system in (6) becomes

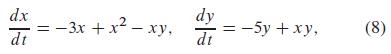
and imply that the three critical points (0,0), (3,0), and (5,2) of (8) are as shown in Fig. 9.3.17-with a nodal sink at the origin, a saddle point on the positive x-axis, and a spiral source at (5,2). In each problem use a graphing calculator or computer system to construct a phase plane portrait for the linearization at the indicated critical point. Do your local portraits look consistent with Fig. 9.3.17?

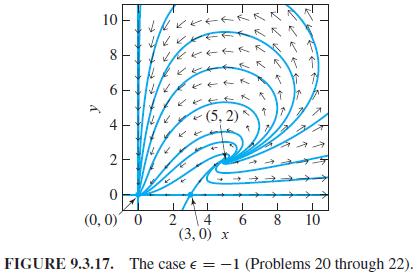
Show that the linearization of (8) at (5,2) is u' = 5u - 5v, v' = 2u. Then show that the coefficient matrix of this linear system has complex conjugate eigenvalues λ₁, λ₂ = 1/2 (5 ± i √15) with positive real part. Hence (5, 2) is a spiral source for the system in (8).

dx dt - 3x + x - xy, dy dt :-5y+xy, (8)