Problems 20 through 22 deal with the case ∈ = -1, for which the system in (6) becomes

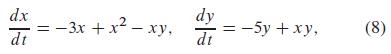
and imply that the three critical points (0,0), (3,0), and (5,2) of (8) are as shown in Fig. 9.3.17-with a nodal sink at the origin, a saddle point on the positive x-axis, and a spiral source at (5,2). In each problem use a graphing calculator or computer system to construct a phase plane portrait for the linearization at the indicated critical point. Do your local portraits look consistent with Fig. 9.3.17?

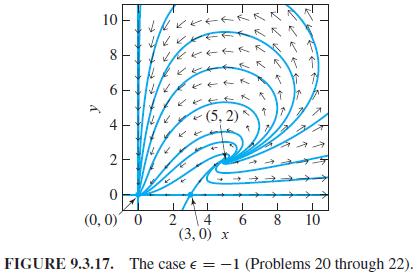
Show that the linearization of the system in (8) at (3,0) is u' = 3u - 3v, v' = -2v. Then show that the coefficient matrix of this linear system has the positive eigenvalue λ₁ = 3 and the negative eigenvalue λ₂ = -2. Hence (3,0) is a saddle point for (8).

dx dt - 3x + x - xy, dy dt :-5y+xy, (8)