Analyze and discuss two limiting cases of Prob. 9–96:

(a) The gap is very small. Show that the velocity profile, approaches linear from the outer cylinder wall to the inner cylinder wall. In other words, for a very tiny gap the velocity profile reduces to that of simple two-dimensional Couette flow. (Define y = R_o – r, h = gap thickness = R_o – R_i, and V = speed of the “upper plate” 5 R_iω_i.) 

(b) The outer cylinder radius approaches infinity, while the inner cylinder radius is very small. What kind of flow does this approach?

Data from Problem 96

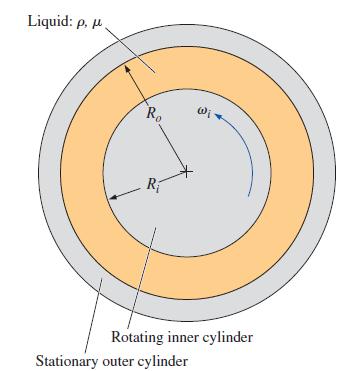
An incompressible Newtonian liquid is confined between two concentric circular cylinders of infinite length— a solid inner cylinder of radius R_i and a hollow, stationary outer cylinder of radius R_o (Fig. P9–96; the z-axis is out of the page). The inner cylinder rotates at angular velocity ω_i. The flow is steady, laminar, and two-dimensional in the r_θ-plane. The flow is also rotationally symmetric, meaning that nothing is a function of coordinate θ (u_θ and P are functions of radius r only). The flow is also circular, meaning that velocity component u_r = 0 everywhere. Generate an exact expression for velocity component u_θ as a function of radius r and the other parameters in the problem. You may ignore gravity.

FIGURE P9–96

Transcribed Image Text:

Liquid: p. p. Ro Wi Rotating inner cylinder Stationary outer cylinder