You will need the results of Prob. 7–63 to do this problem. A tiny aerosol particle falls at steady settling speed V. The Reynolds number is small enough that the creeping flow approximation is valid. If the particle size is doubled, all else being equal, by what factor will the settling speed go up? If the density difference (ρ_p – ρ) is doubled, all else being equal, by what factor will the settling speed go up?

Data from Problem 63

Combine the results of Probs. 7–61 and 7–62 to generate an equation for the settling speed V of an aerosol particle falling in air (Fig. P7–62). Verify that your result is consistent with the functional relationship obtained in Prob. 7–62. For consistency, use the notation of Prob. 7–62.

Data from problem 61

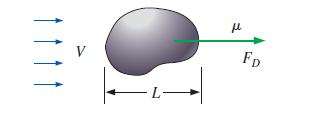
When small aerosol particles or microorganisms move through air or water, the Reynolds number is very small (Re ≪ 1). Such flows are called creeping flows. The aerodynamic drag on an object in creeping flow is a function only of its speed V, some characteristic length scale L of the object, and fluid viscosity μ (Fig. P7–61). Use dimensional analysis to generate a relationship for F_D as a function of the independent variables.

FIGURE P7–61

Data from Problem 62

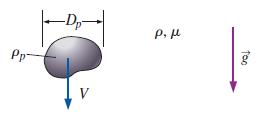
A tiny aerosol particle of density ρ_p and characteristic diameter D_p falls in air of density ρ and viscosity μ (Fig. P7–62). If the particle is small enough, the creeping flow approximation is valid, and the terminal settling speed of the particle V depends only on D_p, μ, gravitational constant g, and the density difference (ρ_p – ρ). Use dimensional analysis to generate a relationship for V as a function of the independent variables. Name any established dimensionless parameters that appear in your analysis.

Fig. P7–62

Transcribed Image Text:

V -L- u FD