Using the distribution function of the previous problem, evaluate the electric current density J to show that the presence of a temperature gradient gives rise to an electric current associated with thermoelectric effects.

Data from problem 10

An electron gas (Lorentz gas), in a background of stationary ions, is acted upon by a weak, externally applied electric field E, under steady state conditions. Using the Boltzmann equation for the electrons, with the relaxation model for the collision term (considering a constant collision frequency ν),

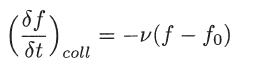
and considering the adiabatic case for which

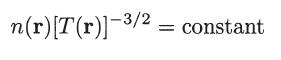
show that the electron distribution function is given by

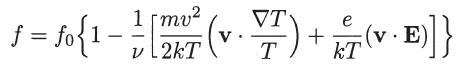
Assume that f = f₀ + f₁, where |f₁| ≪ f₀ and where f₀ is the following modified Maxwellian distribution

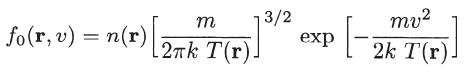
and neglect all second-order terms in the Boltzmann equation. Consider the term involving ∇f₁ as a second-order quantity.

(St) coll = -v(f-fo)