As discussed in the text, spinning black holes contain a considerable amount of rotational energy [Eq. (26.86)].

Question:

As discussed in the text, spinning black holes contain a considerable amount of rotational energy [Eq. (26.86)]. This exercise sketches how this energy may be extracted by an electromagnetic field: the Blandford-Znajek process.

(a) Suppose that a Kerr black hole, described using Boyer-Lindquist coordinates {t , r , θ , ∅}, is orbited by a thick accretion disk (Ex. 26.18), whose surface near the hole consists of two funnels, axisymmetric around the hole’s rotation axis θ = 0 andθ = π. Suppose, further, that the funnels’ interiors contain a stationary, axisymmetric electromagnetic field described by a vector potential A_α(r , θ). The surface of each funnel contains surface current and charge that keep the disk’s interior free of electromagnetic field, and the disk’s gas supplies pressure across the funnel’s surface to balance the electromagnetic stress. Whatever plasma there may be inside the funnel has such low density that the electromagnetic contribution to the stress-energy tensor is dominant, and so we can write F_αβJ^β = 0 [cf. Eq. (2.81b)]. Show that the electromagnetic field tensor [Eq. (25.61)] in the Boyer-Lindquist coordinate basis can be written F_αβ = A_β,α − A_α,β,where the commas denote partial derivatives.

(b) Write A∅ = Ф/(2π), A_t = −V , and by considering the electromagnetic field for r ≫ M, interpret Φ and V as the magnetic flux contained in a circle of fixed r , θ and the electrical potential of that circle, respectively. This also remains true near the black hole, where we define the magnetic and electric fields as those measured by observers who move orthogonally to the hypersurfaces of constant Boyer-Lindquist time t, so E(vector) and B(vector) can be regarded as spatial vectors E and B that lie in those hypersurfaces of constant t. Can you prove all this?

(c) Explain why it is reasonable to expect the electric field E to be orthogonal to the magnetic field B near the hole as well as far away, and use Faraday’s law to show that its toroidal component E∅̂ must vanish. Thereby conclude that the equipotential surfaces V = constant coincide with the magnetic surfaces Φ = constant.

(d) Define an angular velocity by Ω = −2πV,_θ/Φ,_θ, show that it, too, is constant on magnetic surfaces, and show that an observer who moves with this angular velocity d∅/dt = Ω measures vanishing electric field. Thereby conclude that the magnetic field lines rotate rigidly with this angular velocity, and deduce an expression for the electric field E in terms of Φ and Ω.

(e) Use the inhomogeneous Maxwell equations to show that the current density J^α describes a flow of charge along the magnetic field lines. Hence calculate the current I flowing inside a magnetic surface. Express B in terms of I and Φ.

(f) Now sketch the variation of the electromagnetic field in the funnel both near the horizon and at a large distance from it, assuming that there is an outward flow of energy and angular momentum.

(g) Use the fact that ∂/∂t and ∂/∂∅ are Killing vectors (Ex. 25.5) to confirm that electromagnetic energy and angular momentum are conserved in the funnels.

(h) We have derived these general principles without giving an explicit solution that demonstrates energy extraction. In order to do this, we must also specify boundary conditions at the horizon of the black hole and at infinity. The former is essentially that the electromagnetic field be nonsingular when measured by an infalling observer or when expressed in Kerr coordinates, for example. The latter describes the flow of energy and angular momentum as outward. Stable
solutions can be exhibited numerically and, typically, they have Ω ∼ 0.3 to 0.5Ω_H. These solutions demonstrate that energy and angular momentum can flow outward across the event horizon so the mass of the black hole gradually decreases. How can this be?

Equations.

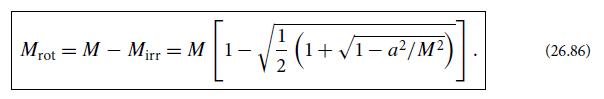
Data from Exercises 26.18.

A quite different type of accretion disk forms when the gas is unable to cool. This can occur when its gas supply rate is either very large or very small. In the former case, the photons are trapped by the inflowing gas; in the latter, the radiative cooling timescale exceeds the inflow timescale. Either way, pressure and gravity are of comparable importance. There is an elegant description of gas flow close to the black hole as a sort of toroidal star, where the metric is associated with the hole and not the gas. In this problem we make simple assumptions to solve for the equilibrium flow.

Data from Exercises 25.5.

A Killing vector field² is a coordinate-independent tool for exhibiting symmetries of the metric. It is any vector field ξ(vector) that satisfies