Suppose that pattern P and text T are randomly chosen strings of length m and n, respectively, from the d-ary alphabet ?_d = {0, 1, . . . , d ? 1}, where d ? 2. Show that the expected number of character-to-character comparisons made by the implicit loop in line 4 of the naive algorithm is

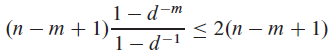
over all executions of this loop. (Assume that the naive algorithm stops comparing characters for a given shift once it finds a mismatch or matches the entire pattern.) Thus, for randomly chosen strings, the naive algorithm is quite efficient.

1d- ( + 1)- < 2( + 1) 1-d-1