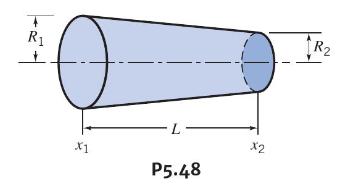
Consider the one-dimensional, incompressible flow through the circular channel shown. The velocity at section (1) is given by \(U=U_{0}+U_{1} \sin \omega t\), where \(U_{0}=20 \mathrm{~m} / \mathrm{s}, U_{1}=2 \mathrm{~m} / \mathrm{s}\), and \(\omega=0.3 \mathrm{rad} / \mathrm{s}\). The channel dimensions are \(L=1 \mathrm{~m}, R_{1}=0.2 \mathrm{~m}\), and \(R_{2}=0.1 \mathrm{~m}\). Determine the particle acceleration at the channel exit. Plot the results as a function of time over a complete cycle. On the same plot, show the acceleration at the channel exit if the channel is constant area, rather than convergent, and explain the difference between the curves.

Transcribed Image Text:

R1 x1 L- P5.48 12 R2