In a single-server queueing system in which customers arrive according to a Poisson process, the long-run average queueing delay per customer depends on the service distribution through its mean and variance. Indeed, if μ is the mean service time, and σ2 is the variance of a service time, then the average amount of time that a customer spends waiting in queue is given by

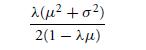
provided that λμ Suppose that the owner of a service station will hire a second server if it can be shown that the average service time exceeds 8 minutes. The following data give the service times (in minutes) of 28 customers of this queueing system. Do they indicate that the mean service time is greater than 8 minutes?
8.6, 9.4, 5.0, 4.4, 3.7, 11.4, 10.0, 7.6, 14.4, 12.2, 11.0, 14.4, 9.3, 10.5, 10.3, 7.7, 8.3, 6.4, 9.2, 5.7, 7.9, 9.4, 9.0, 13.3, 11.6, 10.0, 9.5, 6.6

2(+0) 2(1 )