Question: Let X be a continuous random variable with probability density function f and assume that a 0 and b are two real numbers. (i)

Let X be a continuous random variable with probability density function f and assume that a ≠ 0 and b are two real numbers.

(i) Show that the probability density fY of the variable Y = aX + b is given by the formula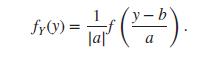fy(y)= =lar (v=b). -b a

(ii) If the probability density of X is given by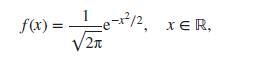image text in transcribed

find the density function of Y = ???? + ????X, where???? > 0 and ???? ∈ ℝ are two real constants.

fy(y)= =lar (v=b). -b a

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Introduction To Probability Statistics Questions!

Q:

This exercise will lead you through a proof of Chebyshevs inequality. Let X be a continuous random variable with probability density function f (x). Suppose that P(X

Q:

6. Let X be a continuous random variable with probability density function f (x ) = be-bx, x>0 ; b>0 elsewhere Find the moment generating function of X, Mx (t) . Then, find M x (-6b). 7. Let X be a...

Q:

22. Let X be a continuous random variable whose probability density function f is even; that is, f (x) = f (x), x. Prove that (a) the random variables X and X have the same probability distribution...

Q:

21. Let X be a continuous random variable with probability density function f . Show that if E(X) exists; that is, if # |x|f (x) dx x) = 0.

Q:

How do I solve this question? 1. Let X be a continuous random variable with probability density function f[$) and distribution function 13(1). Show that an a. E R minimizing E|X {1| sat. ises F(n] =...

Q:

Practice Exam 1 1. (19 total points) PROBABILITY CALCULATIONS Let X be a continuous random variable with probability density function f (x) = 3x2 , for 0 x 1 . 2.0 1.0 0.0 f(x) = 3x2 3.0 Here is a...

Q:

9. Let X be a continuous random variable with probability density function f.We say that X is symmetric about if for all x, (a) Prove that X is symmetric about if and only if for all x, we have f( ...

Q:

Let X be a continuous random variable with probability density function f(x) and cumulative probability distribution function I Let I be a continuous random variable with probability density function...

Q:

Let X be a continuous random variable with probability density function f(x) and cumulative probability distribution function F(x). I Let I be a continuous random variable with probability density...

Q:

Econ 2500 Section D 3.0 - Fall 2016 Assignment 2 (Due Date: November 24, 2015) Question 1: Let X be a continuous random variable with probability density function 0

Q:

A radio is marked up 65% of the selling price. Find the equivalent markup rate based on the cost. Round to the nearest tenth of a percent.

Q:

Kathy purchased a new car for $37,800. From her research she has determined that it straight-line depreciates over 14 years. She made a $7,000 down payment and pays $710 per month for her car loan....

Q:

should an impairment on an long term asset be recorded when the fair value has temporarily decreased below historical cost

Q:

What is the definition of cooperative strategy, and why is this strategy important to firms competing in the current competitive landscape?

Q:

A professor continually gives exams to her students. She can give three possible types of exams, and her class is graded as either having done well or badly. Let p, denote the probability that the...

Q:

Each of two switches is either on or off during a day. On day n, each switch will independently be on with probability [1+ number of on switches during day n - 11/4 For instance, if both switches are...

Q:

A certain town never has two sunny days in a row. Each day is classified as being either sunny, cloudy (but dry), or rainy. If it is sunny one day, then it is equally likely to be either cloudy or...

Q:

12 1 pt Which of the following is closest to the y-intercept of the regression equation pictured below? 0 0 50 100 75 F5 15 300- Assault 100- 10 Murder 15

Q:

Engines Done Right Co. is trying to establish the standard labor cost of a typical engine tune-up. The following data have been collected from time and motion studies conducted over the past month....

Q:

22 Help Save & Saved TB MC Qu. 18-114 (Algo) Maroon Company's contribution... Maroon Company's contribution margin ratio is 36%. Total fixed costs are $147,600. What is Maroon's break-even point in...