(a) Generalize Problem 8.2, using the trial wave function for arbitrary n.

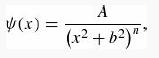
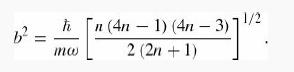
(b) Find the least upper bound on the first excited state of the harmonic oscillator using a trial function of the form

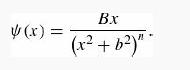
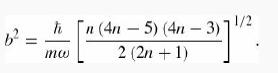
(c) Notice that the bounds approach the exact energies as n → ∞ . Why is that? Plot the trial wave functions for n = 2, n = 3, and n = 4, and compare them with the true wave functions (Equations 2.60 and 2.63). To do it analytically, start with the identity

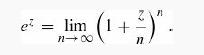
V(x) = A (x + b)"