The two-body integrals D 2 and 2 are defined in Equations 8.65 and 8.66. To evaluate D 2 we write where 2 is

The two-body integrals D₂ and χ₂ are defined in Equations 8.65 and 8.66. To evaluate D₂ we write

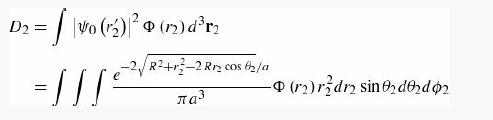
where θ₂ is the angle between R and r₂ (Figure 8.8), and

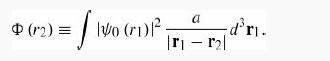
(a) Consider first the integral over r₁. Align the z axis with r₂ (which is a constant vector for the purposes of this first integral) so that

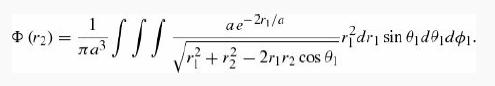
Do the angular integration first and show that

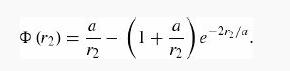
(b) Plug your result from part (a) back into the relation for D₂, and show that

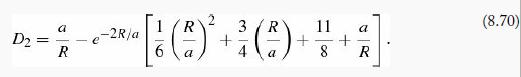
Again, do the angular integration first.
Comment: The integral χ₂ can also be evaluated in closed form, but the procedure is rather involved. We will simply quote the result,

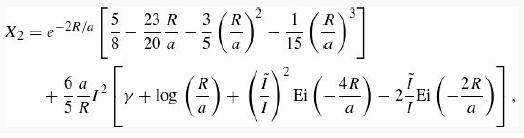
where ϒ = 0.5772 ... is Euler’s constant, Ei(x) is the exponential integral (8.71)

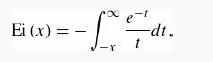
and Î is obtained from I by switching the sign of R:

= [ 4/ (1) 9 (1) dm = [[[ D2 -2/R+2-2 Rn cos /a - (r) rdr sinondo2d2