(a) Show that the most general density matrix for a spin-1/2 particle can be written in terms of three real numbers ( 1 , 2

(a) Show that the most general density matrix for a spin-1/2 particle can be written in terms of three real numbers (α₁,α₂,α₃):

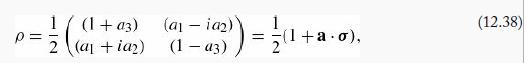
where σ₁,σ₂,σ₃ are the three Pauli matrices.

(b) In the literature, a is known as the Bloch vector. Show that ρ represents a pure state if and only if |a| = 1, and for a mixed state |a| (c) What is the probability that a measurement of S_z would return the value +ћ/2, if the tip of the Bloch vector is at (i) the north pole (a = (0,0, 1)), (ii) the center of the sphere (a = (0,0,0)), (iii) the south pole (a = (0,0, -1))?

(d) Find the spinor χ representing the (pure) state of the system, if the Bloch vector lies on the equator, at azimuthal angle ϕ.

Problem 12.6 (c)

(c) Show that  ρ² = ρ if and only if ρ represents a pure state.

p= 1 / (1+03) 2 (a1 + ia) ()). (a - ia) (1-a3) = (1+a.o), (12.38)