Consider operators  and B̂ that do not commute with each other  but do commute with their commutator: 

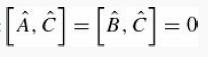
(for instance, x̂ and p̂).

(a) Show that

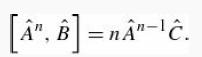
You can prove this by induction on n, using Equation 3.65.

(b) Show that

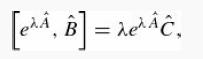
where λ is any complex number. Express e^λ as a power series.
(c) Derive the Baker–Campbell–Hausdorff formula:

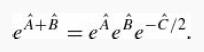
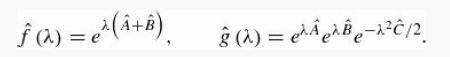
these functions are equal at λ = 0, and show that they satisfy the same differential equation: 

and

Therefore, the functions are themselves equal for all λ.

Equation 3.65

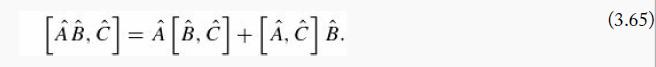
(C = [A, B])