Question: For the examples in Problem 11.24 (c) and (d), calculate C m (t), to first order. Check the normalization condition: and comment on any discrepancy.

For the examples in Problem 11.24 (c) and (d), calculate C_m(t), to first order. Check the normalization condition:

012 = 1, m (11.122)

and comment on any discrepancy. Suppose you wanted to calculate the probability of remaining in the original state Ψ_N; would you do better to use

Problem 11.24 (c) and (d)

(c) For example, suppose Ĥ' is constant (except that it was turned on at t = 0, and switched off again at some later time . Find the probability of transition from state N to state M (M ≠ N), as a function of T.

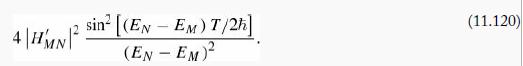
(d) Now suppose Ĥ' is a sinusoidal function of time: Ĥ' = VCos(ωt). Making the usual assumptions, show that transitions occur only to states with energy EM = EN ± ћω, and the transition probability is

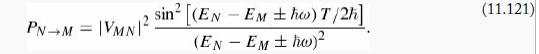
012 = 1, m (11.122)

Step by Step Solution

★★★★★

3.45 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

For example c This is plainly greater than 1 But remember The cs are accurate only ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Introduction To Quantum Mechanics Questions!

Show (BA) T = AB for A and B in Example 2, for any n X n Hermitian A and skew-Hermitian B.

Suppose that T is n n and c, d are scalars. (a) Prove that if T has the eigenvalue with an associated eigenvector v then v is an eigenvector of cT + dI associated with eigenvalue c + d. (b) Prove...

Suppose CA = Im, where C is m Ã n and A is n Ã m. Consider the system AX = B of n equations in m variables. If find X (if it exists) when (i) (ii) 2 -3 0-S 1 3 0 -1 I and A=| 1-2 6 -10...

can someone solve this Modern workstations typically have memory systems that incorporate two or three levels of caching. Explain why they are designed like this. [4 marks] In order to investigate...

UNIT 5 QZ, Q-20 UNIT 5 / UNIT 8 QUESTIONS KEEP ANSWERS SEPARATE BY UNITS UNIT II STUDY GUIDE Consumer Mathematics Reading Assignment See information below. Key Terms 1. Add-on interest method 2....

HW 12, MAT 312/AMS 351: SPRING 2017 Problem 1. (1) Set H = {4a + 6b | a, b Z} Z. Show that H is a subgroup of Z. (2) Is H cyclic? Problem 2. Write down all the cyclic subgroups of the following...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

You own a small storefront retail business and are interested in determining the average amount of money a typical customer spends per visit to your store. You take a random sample over the course of...

Last Updated: July 18, 2016 American Mock Trial Association MIDLANDS RULES OF EVIDENCE Article I. Rule 101. Scope; Definitions (a) Scope. These rules apply to proceedings in the courts of the State...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

Techno Company produces a regular computer monitor that sells for $175 and a flat panel computer monitor that sells for $300. Last year, total overhead costs of $3,675,000 were allocated based on...

In the 30 June 2019 annual report of Avoca Ltd, the equipment was reported as follows: Equipment (at cost) Accumulated depreciation 1,950,000 595,000 1,355,000 The equipment consisted of two...

Unlike manufacturing companies, the majority of a commercial bank's liabilities are Blank _ _ _ _ _ _ and Blank _ _ _ _ _ _ . Multiple choice question. long - term deposits; short - term borrowings...

Can a service duration be more variable than an Exponential distribution? Explain.

A company must purchase ve kinds of material. The following table gives the price the company pays per ton for each material, along with the number of tons purchased in the months of May, June, and...

A fenced enclosure consists of a rectangle of length L and width 2R, and a semicircle of radius R, as shown in Figure P20. The enclosure is to be built to have an area A of 1600 ft 2 . The cost of...

A water tank consists of a cylindrical part of radius r and height h, and a hemispherical top. The tank is to be constructed to hold 500 m 3 of fluid when filled. The surface area of the cylindrical...

5. A firm has a sales of Rs. 60,00,000, variable cost is 20% on sales, fixed cost is Rs. 20,50.000 and debentures of Rs. 8.00.000 at 10% rate of interest. Calculate Operating leverage, financial...

Koban Corp. currently has an all-cash credit policy. It is considering making a change in the credit policy by going to terms of net 90 days (Assume there are 30 days in each month). The required...

The table below lists the independent projects that your company is considering to invest: Project Initial investment (USD) NPV (USD) IRR (%) A 510000 -50240 12.23 B 270000 62331 14.83 C 420000 60342...