Sequential measurements. An operator A, representing observable A, has two (normalized) eigenstates 1 and 2

Sequential measurements. An operator Â, representing observable A, has two (normalized) eigenstates Ψ₁ and Ψ₂, with eigenvalues α₁ and α₂, respectively. Operator B̂, representing observable B, has two (normalized) eigenstates ∅₁ and ∅₂, with eigenvalues b₁ and b₂. The eigenstates are related by

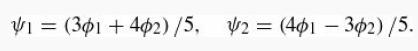(a) Observable A is measured, and the value is obtained. What is the state of the system (immediately) after this measurement?
(b) If B is now measured, what are the possible results, and what are their probabilities?
(c) Right after the measurement of B, A is measured again. What is the probability of getting a₁?

Transcribed Image Text:

V1 = (301 +402)/5, 2= (401 - 302)/5.