Suppose you wanted to describe an unstable particle, that spontaneously disintegrates with a lifetime . In that

Suppose you wanted to describe an unstable particle, that spontaneously disintegrates with a “lifetime” τ. In that case the total probability of finding the particle somewhere should not be constant, but should decrease at (say) an exponential rate:

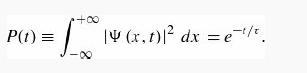
A crude way of achieving this result is as follows. In Equation 1.24 we tacitly assumed that V (the potential energy) is real. That is certainly reasonable, but it leads to the “conservation of probability” enshrined in Equation 1.27. What if we assign to V an imaginary part:

where V₀ is the true potential energy and Γ is a positive real constant?
(a) Show that (in place of Equation 1.27) we now get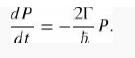
(b) Solve for p(t), and find the lifetime of the particle in terms of Γ.

Equation 1.24

Equation 1.27

Transcribed Image Text:

+00 P(t) = =√ 14 (x,1) 1² dx = e ¹/6. 88