This problem is designed to guide you through a “proof” of Plancherel’s theorem, by starting with the theory of ordinary Fourier series on a finite interval, and allowing that interval to expand to infinity.
(a) Dirichlet’s theorem says that “any” function f(x) on the interval [-α +α] can be expanded as a Fourier series:

Show that this can be written equivalently as

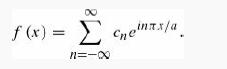
What is c_n , in terms of  α_n and b_n ?
(b) Show (by appropriate modification of Fourier’s trick) that

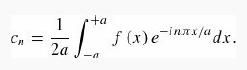
(c) Eliminate n and  c_n in favor of the new variables k = (nπ/α) and 

Show that (a) and (b) now become

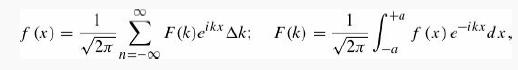
where Δk is the increment in k from one n to the next.
(d) Take the limit  to obtain Plancherel’s theorem. Comment: In view of their quite different origins, it is surprising (and delightful) that the two formulas—one for F(k) in terms of f(x), the other for f(x) in terms of F(k) —have such a similar structure in the limit
.

Transcribed Image Text:

-Σ[{")+40(**)]. «nsin h, Cos a f(x) = n=0 ηπ