One consequence of defining the cumulant generating function in terms of the moment generating function is that
Question:
One consequence of defining the cumulant generating function in terms of the moment generating function is that the cumulant generating function will not exist any time the moment generating function does not. An alternate definition of the cumulant generating function is defined in terms of the characteristic function. That is, if \(X\) has characteristic function \(\psi(t)\), then the cumulant generating function can be defined as \(c(t)=\log [\psi(t)]\).
a. Assume all of the cumulants (and moments) of \(X\) exist. Prove that the coefficient of \((i t)^{k} / k\) ! for the cumulant generating function defined using the characteristic function is the \(k^{\text {th }}\) cumulant of \(X\). You may want to use Theorem 2.31.
b. Find the cumulant generating function of a random variable \(X\) that has a \(\operatorname{Cauchy}(0,1)\) distribution based on the fact that the characteristic function of \(X\) is \(\psi(t)=\exp (|t|)\). Use the form of this cumulant generating function to argue that the cumulants of \(X\) do not exist.
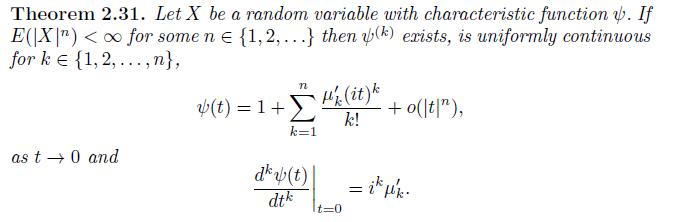
Step by Step Answer:






