Prove the second part of Theorem 3.8. That is let (left{X_{n}ight}_{n=1}^{infty}) be a sequence of random variables,
Question:
Prove the second part of Theorem 3.8. That is let \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of random variables, \(X\) be a random variable, and \(g\) be a Borel function on \(\mathbb{R}\). Let \(C(g)\) be the set of continuity points of \(g\) and suppose that \(P[X \in\) \(C(g)]=1\). Prove that if \(X_{n} \xrightarrow{p} X\) as \(n ightarrow \infty\), then \(g\left(X_{n}ight) \xrightarrow{p} g(X)\) as \(n ightarrow \infty\). Hint: Prove by contradiction using Theorem 3.5.
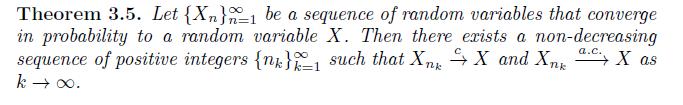
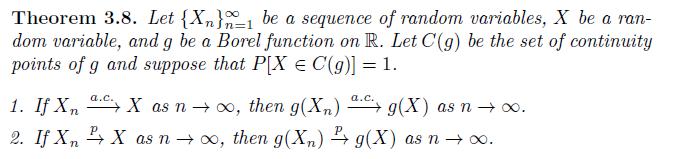
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





