Let \(\boldsymbol{A} \mathbf{x}=\mathbf{b}\) be the system of equality constraints for a standard maximum problem, after the introduction of slack variables. There are \(n\) variables and \(m\) constraints. A basic solution is a vector \(\mathbf{x}\) that satisfies the equality constraints, and has \(n-m\) of its components equal to 0 , but is not required to satisfy the non-negativity constraint. For each basic solution of the maximum problem, there is a complementary basic solution (again, not necessarily feasible) for its dual minimum problem, obtained by reading the negatives of the slack coefficients in the objective row of the corresponding maximum simplex system. To see what basic solutions represent in two dimensions, consider the problem:

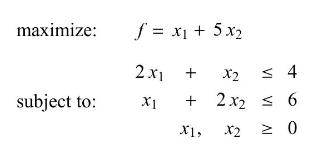
(a) Write the dual problem, and sketch the feasible regions for both problems. In each case find the coordinates of all corner points, whether feasible or infeasible.

(b) Write a simplex system for each basic solution of the maximum problem, and find the point on each graph to which the system corresponds.

Transcribed Image Text:

maximize: f = x1 + 5x2 2.01 + X2 4 + 2x2 6 X1, *2 0 X2 subject to: X1