Consider the regression model \(W A G E=\beta_{1}+\beta_{2} E D U C+e\). Where \(W A G E\) is hourly wage rate in US 2013 dollars. EDUC is years of schooling. The model is estimated twice, once using individuals from an urban area, and again for individuals in a rural area.

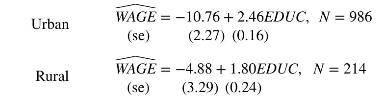
a. Using the urban regression, test the null hypothesis that the regression slope equals 1.80 against the alternative that it is greater than 1.80. Use the \(\alpha=0.05\) level of significance. Show all steps, including a graph of the critical region and state your conclusion.

b. Using the rural regression, compute a \(95 \%\) interval estimate for expected \(W A G E\) if \(E D U C=16\). The required standard error is 0.833. Show how it is calculated using the fact that the estimated covariance between the intercept and slope coefficients is -0.761 .

c. Using the urban regression, compute a \(95 \%\) interval estimate for expected \(W A G E\) if \(E D U C=16\). The estimated covariance between the intercept and slope coefficients is -0.345 . Is the interval estimate for the urban regression wider or narrower than that for the rural regression in (b). Do you find this plausible? Explain.

d. Using the rural regression, test the hypothesis that the intercept parameter \(\beta_{1}\) equals four, or more, against the alternative that it is less than four, at the \(1 \%\) level of significance.

Urban Rural = WAGE -10.76+ 2.46EDUC, N = 986 (2.27) (0.16) (se) WAGE = -4.88 +1.80EDUC, N = 214 (se) (3.29) (0.24)