Consider the regression model \(W A G E=\beta_{1}+\beta_{2} E D U C+e\) where \(W A G E\) is hourly wage rate in U.S. 2013 dollars, \(E D U C\) is years of education attainment. The model is estimated twice, once using individuals from an urban area, and again for individuals in a rural area.

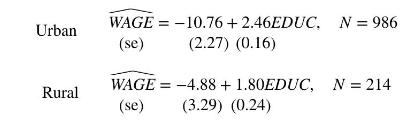
a. For the rural regression, compute a \(95 \%\) prediction interval for \(W A G E\) if \(E D U C=16\), and the standard error of the forecast is 9.24 . The standard error of the regression is \(\hat{\sigma}=9.20\) for the rural data.

b. For the urban data, the sum of squared deviations of EDUC about its sample mean is 8435.46 and the standard error of the regression is \(\hat{\sigma}=14.25\). The sample mean wage in the urban area is \(\$ 24.49\). Calculate the \(95 \%\) prediction interval for \(W A G E\) if \(E D U C=16\). Is the interval wider or narrower than the prediction interval for the rural data? Do you find this plausible? Explain.

WAGE -10.76 +2.46EDUC, N = 986 Urban (se) Rural (2.27) (0.16) WAGE=-4.88 +1.80EDUC, N = 214 (se) (3.29) (0.24)