Consider the regression model (y_{i}=beta_{1}+beta_{2} x_{i}+beta_{3} z_{i}+e_{i}), where (Eleft(e_{i} mid mathbf{X} ight)=0, operatorname{var}left(e_{i} mid mathbf{X} ight)=sigma^{2}), and

Consider the regression model \(y_{i}=\beta_{1}+\beta_{2} x_{i}+\beta_{3} z_{i}+e_{i}\), where \(E\left(e_{i} \mid \mathbf{X}\right)=0, \operatorname{var}\left(e_{i} \mid \mathbf{X}\right)=\sigma^{2}\), and \(E\left(e_{i} e_{j} \mid \mathbf{X}\right)=0\) for \(i eq j\), with \(\mathbf{X}\) representing all observations on \(x\) and \(z\). Suppose \(z_{i}\) is omitted from the equation, so that we have the least squares estimator for \(\beta_{2}\) as

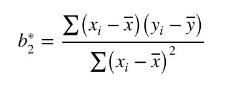Prove that

a. \(b_{2}^{*}=\beta_{2}+\beta_{3} \sum w_{i} z_{i}+\sum w_{i} e_{i}\), where \(w_{i}=\left(x_{i}-\bar{x}\right) / \sum\left(x_{i}-\bar{x}\right)^{2}\).

b. \(E\left(b_{2}^{*} \mid \mathbf{X}\right)=\beta_{2}+\beta_{3} \widehat{\operatorname{cov}}(x, z) / \widehat{\operatorname{var}}(x)\)

c. \(\operatorname{var}\left(b_{2}^{*} \mid \mathbf{X}\right)=\sigma^{2} /(N \widehat{\operatorname{var}}(x))\)

d. \(\operatorname{var}\left(b_{2}^{*} \mid \mathbf{X}\right) \leq \operatorname{var}\left(b_{2} \mid \mathbf{X}\right)\), where \(b_{2}\) is the least squares estimator with both \(x\) and \(z\) included.

Transcribed Image Text:

b = (x) (y) (; - 7) 2