Let y be any response variable and x a binary explanatory variable. Let {(x_i, y_i): i = 1, ... , n} be a sample of size n. Let n₀ be the number of observations with x_i = 0 and n₁ the number of observations with x_i = 1. Let y₀ be the average of the y̅_i with x_i = 0 and y̅₁ the average of the y_i with x_i = 1.

(i) Explain why we can write

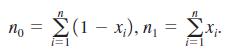
Show that x̅ = n₁/n and (1 – x) 5 n₀/n. How do you interpret x̅?

(ii) Argue that

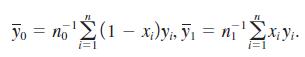
(iii) Show that the average of y_i in the entire sample, y̅, can be written as a weighted average:

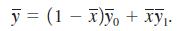
(iv) Show that when xi is binary,

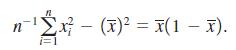
(v) Show that

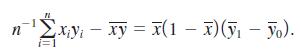
(vi) Use parts (iv) and (v) to obtain (2.74).

(vii) Derive equation (2.73).

2(1 x,), n, = i=1